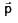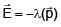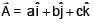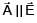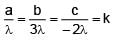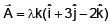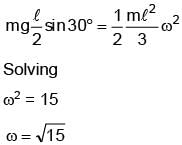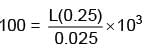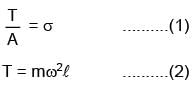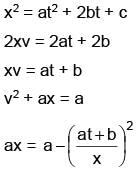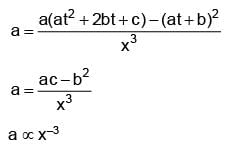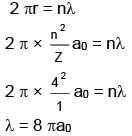JEE Main 2020 Question Paper with Solution (9th January - Morning) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Main 2020 Question Paper with Solution (9th January - Morning)
Kinetic energy of the particle is E and it's De–Broglie wavelength is λ. On increasing it's KE by ΔE, it's new De–Broglie wavelength becomes λ/2 . Then ΔE is
The dimensional formula of 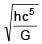 is
is
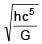 is
is| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
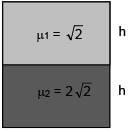
Two immiscible liquids of refractive index √2 and 2√2 are filled with equal height h in a vessel. Then apparent depth of bottom surface of the container given that outside medium is air:
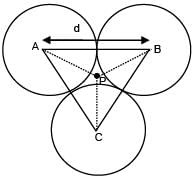
Three identical solid spheres each having mass 'm' and diameter 'd' are touching each other as shown in figure. Calculate ratio of moment of inertia about an axis (perpendicular to plane of paper) passing through point P and B as shown in figure. Given P is centroid of triangle ABC.
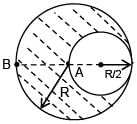
A solid sphere having radius R and Uniform charge density ρ has a cavity of radius R/2 as shown in figure. Find the ratio of magnitude of electric field at point A and B i.e.
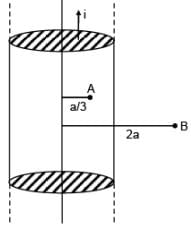
Consider an infinitely long current carrying cylindrical straight wire having radius 'a'. Then the ratio of magnetic field at distance a/3 and 2a from axis of wire is.
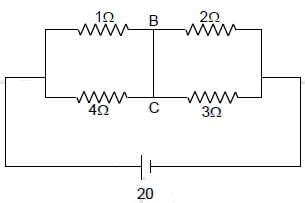
Find current in the wire BC.
Two electromagnetic waves are moving in free space whose electric field vectors are given by 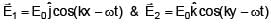 . A charge q is moving with velocity
. A charge q is moving with velocity 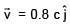 .Find the
.Find the
net Lorentz force on this charge at t = 0 and when it is at origin.
Two ideal di-atomic gases A and B. A is rigid, B has an extra degree of freedom due to vibration. Mass of A is m and mass of B is m/4. The ratio of molar specific heat of A to B at constant volume is :
An ideal liquid (water) flowing through a tube of non uniform cross section area at A and B are 40 cm2 and 20 cm2 respectively. If pressure difference between A & B is 700 N/m2 then volume flow rate is :
A screw gauge adv ances by 3mm in 6 rotations. There are 50 divisions on circular scale. Find least count of screw gauge ?
A telescope of aperture diameter 5m is used to observe the moon from the earth. Distance between the moon and earth is 4 × 105 km. Determine the minimum distance between two points on the moon's surface which can be resolved using this telescope. (Wave length of light is 5893 Å).
A particle of mass m is revolving around a planet in a circular orbit of radius R. At the instant the particle has velocity 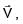 another particle of mass m/2 moving at velocity
another particle of mass m/2 moving at velocity 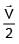 collides perfectly in-elastically with the first particle. The new path of the combined body will take is
collides perfectly in-elastically with the first particle. The new path of the combined body will take is
Two particles of same mass 'm' moving with velocities 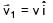 and
and 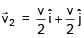 collide in-elastically. Find the loss in kinetic energy.
collide in-elastically. Find the loss in kinetic energy.
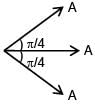
Three wav es of same intensity (I0) having initial phases 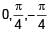 rad respectively interfere at a point.Find the resultant Intensity
rad respectively interfere at a point.Find the resultant Intensity
Particle moves from point A to point B along the line shown in figure under the action of force. 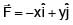 . Determine the work done on the particle by
. Determine the work done on the particle by 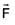 in moving the particle from point A to point B
in moving the particle from point A to point B
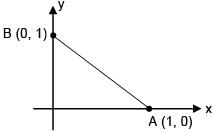
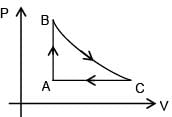
For the given P-V graph for an ideal gas, chose the correct V- T graph. Process BC is adiabatic.
Given . Find vector parallel to electric field at position
. Find vector parallel to electric field at position 
[Note that 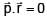 ]
]
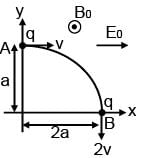
Which of the following statements are correct for moving charge as shown in figure.
Photons of wav elength 6556 Å falls on a metal surface. If ejected electrons with maximum K.E. moves in magnetic field of 3 × 10–4 T in circular orbit of radius 10–2m, then work function of metal surface is
A rod of length 1 m is released from rest as shown in the figure below.

If ω of rod is √n at the moment it hits the ground, then find n.
If reversible voltage of 100 V is applied across an inductor, current in it reduces from 0.25A to 0A in 0.025ms. Find inductance of inductor (in mH).
A wire of length l = 3m and area of cross section 10–2cm2 and breaking stress 48×107N/m2 is attached with block of mass 10kg. Find the maximum possible value of angular velocity with which block can be moved in circle with string fixed at one end.
Position of a particle as a function of time is given as x2 = at2 + 2bt + c, where a, b, c are constants. Acceleration of particle varies with x–n then value of n is.
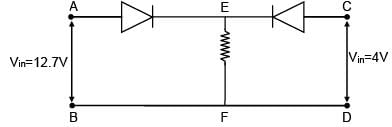
In the given circuit both diodes having zero forward resistance and built-in potential of 0.7 V. Find the potential of point E in volts.
Determine wavelength of electron in 4th Bohr's orbit ?
Which of the following species have one unpaired electron each?
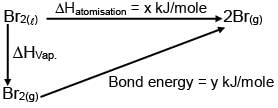
For Br2(l) Enthalpy of atomisation = x kJ/mol Bond dissociation enthalpy of bromine = y kJ/mole
then
Which of the following oxides are acidic, Basic Amphoteric Respectively.
Complex Cr(H2O)6Cln shows geometrical isomerism and also reacts with AgNO3 solution.
Given : Spin only magnetic moment = 3.8 B.M.
What is the IUPAC name of the complex.
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


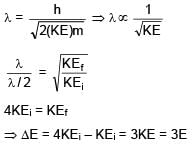
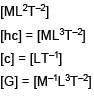
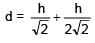
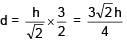
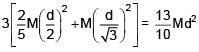

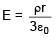
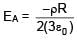
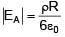
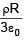
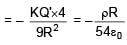
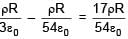
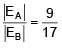
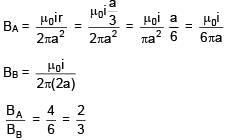

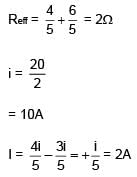
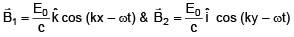
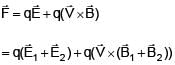
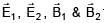
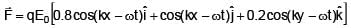
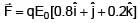
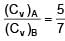
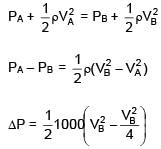
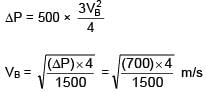
 =
=  = 0.01 mm = 0.001 cm
= 0.01 mm = 0.001 cm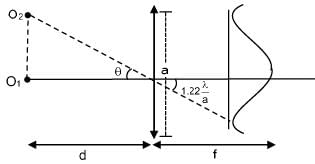
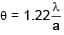
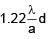
 ≈ 57.5 m
≈ 57.5 m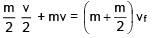

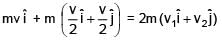
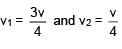
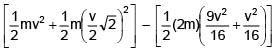
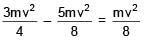
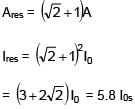

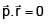
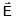 must be antiparallel to
must be antiparallel to