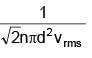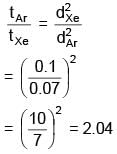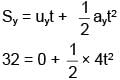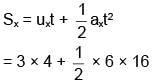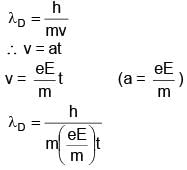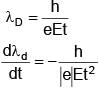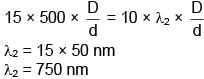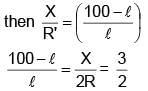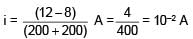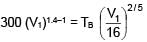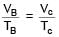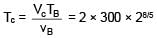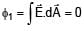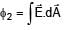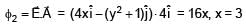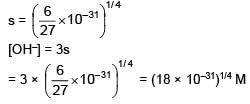JEE Main 2020 Question Paper with Solution (9th January - Evening) - JEE MCQ
30 Questions MCQ Test Additional Study Material for JEE - JEE Main 2020 Question Paper with Solution (9th January - Evening)
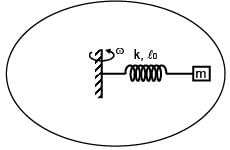
A mass m attached to spring of natural length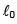 and spring constant k.One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k >> mω2) :
and spring constant k.One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k >> mω2) :
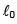 and spring constant k.One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k >> mω2) :
and spring constant k.One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k >> mω2) :A loop of radius R and mass m is placed in a uniform magnetic field B with its plane perpendicular to the field. Current I is flowing in it. Now loop is slightly rotated about its diameter and released. Find time period of oscillation.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A string of mass per unit length μ = 6 × 10–3 kg/m is fixed at both ends under the tension 540 N. If the string is in resonance with consecutive frequencies 420 Hz and 490 Hz. Then find the length of the string?
Ratio of energy density of two steel rods is 1 : 4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
A particle is projected from the ground with speed u at angle 60° from horizontal. It collides with a second particle of same mass moving with horizontal speed u in same direction at highest point of its trajectory. If collision is perfectly inelastic then find horizontal distance travelled by them after collision when they reached at ground
H-like atom with ionization energy of 9R. Find the wavelength of light emitted (in nm) when electron jumps from second excited state to ground state. (R is Rydberg constant)
Two planets of masses M and M/2 have radii R and R/2 respectively. If ratio of escape velocities from their surfaces v1/v2 is n/4, then find n :
Find centre of mass of given rod of linear mass density λ = 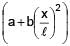 , x is distance from one of its end. Length of the rod is l.
, x is distance from one of its end. Length of the rod is l.
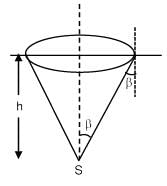
If a point source is placed at a depth h in a liquid of refractive index 4/3. Find percentage of energy of light that escapes from liquid. (assuming 100% transmission of emerging light)
System is released from rest. Moment of inertia of pulley 'I'. Find angular speed of pulley when m1 block falls by 'h'. (Given m1 > m2 and assume no slipping between string and pulley).

Find the current supplied by the battery?
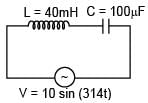
An AC source is connected to the LC series circuit with V = 10 sin (314t). Find the current in the circuit as function of time ? (L = 40 mH, C = 100 μF)
There is a long solenoid of radius ‘R’ having ‘n’ turns per unit length with current i flowing in it. A particle having charge ‘q’ and mass ‘m’ is projected with speed 'v' in the perpendicular direction of axis from a Point on its axis Find maximum value of 'v' so that it will not collide with the solenoid.
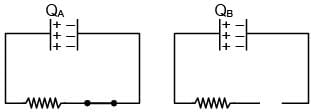
A Capacitor C and resister R are connected to a battery of 5V in series. Now battery is disconnected and a diode is connected as shown in figure (a) and (b) respectively. Then charge on the capacitor after time RC in (a) and (b) respectively is QA and QB. Their value are
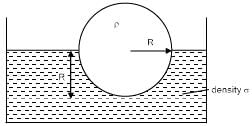
A sphere of density ρ is half submerged in a liquid of density σ and surface tension T. The sphere remains in equilibrium. Find radius of the sphere (assume the force due to surface tension acts tangentially to surface of sphere)
An EM wave is travelling in 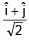 direction. Axis of polarization of EM wave is found to be
direction. Axis of polarization of EM wave is found to be 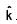 Then equation of magnetic field will be
Then equation of magnetic field will be
Different value of a, b and c are given and their sum is d. Arrange the value of d in increasing order
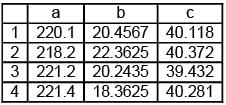
Two gases Ar (40) and Xe (131) at same temperature have same number density. Their diameters are 0.07 nm and 0.10 nm respectively. Find the ratio of their mean free time
A particle starts moving from origin with velocity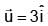 from origin and acceleration
from origin and acceleration 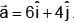 . Find x-coordinate at the instant when y-coordinate of the particle is 32 m.
. Find x-coordinate at the instant when y-coordinate of the particle is 32 m.
An electron  is released in Electric field E from rest. Rate of change of de-Broglie wavelength with time will be.
is released in Electric field E from rest. Rate of change of de-Broglie wavelength with time will be.
In YDSE pattern with light of wavelength λ1 = 500nm, 15 fringes are obtained on a certain segment of screen. If number of fringes for light of wavelength λ2 on same segment of screen is 10, then the value of λ2 (in nm) is-
If in a meter bridge experiment, the balancing length ' l ' was 25 cm for the situation shown in the figure. If the length and diameter of the of wire of resistance R is made half, then find the new balancing length in centimetre is
Find the power loss in each diode (in mW), if potential drop across the zener diode is 8V.

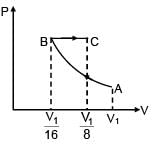
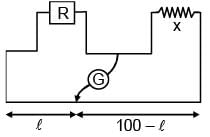
An ideal gas at initial temperature 300 K is compressed adiabatically 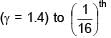 of its initial volume. The gas is then expanded isobarically to double its volume. Then final temperature of gas round to nearest integer is:
of its initial volume. The gas is then expanded isobarically to double its volume. Then final temperature of gas round to nearest integer is:
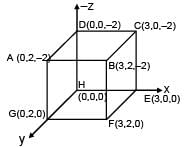
If electric field in the space is given by 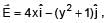 and electric flux through ABCD is φ1 and electric flux through BCEF is φ2 , then find (φ1 - φ2)
and electric flux through ABCD is φ1 and electric flux through BCEF is φ2 , then find (φ1 - φ2)
5 g of Zn reacts with
(I) Excess of NaOH (II) Dilute HCl, then volume ratio of H2 gas evolved in (I) and (II) is
Given Ksp for Cr(OH)3 is 6 × 10–31 then determine [OH–].
(Neglect the contribution of OH– ions from H2O)
Select the correct statements among the followings
(A) LiCl does not dissolve in pyridine
(B) Li does not react ethyne to form ethynide.
(C) Li and Mg react slowly with water.
(D) Among alkali metals Li has highest hydration tendency.
Given an element having following ionisation enthalpies IE1 = 496 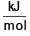 and IE2 = 4562
and IE2 = 4562 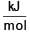 one mole
one mole
hydroxide of this element is treated separated with HCl and H2SO4 respectiv ely. Moles of HCl and H2SO4 reacted respectively is
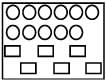
Reactant A represented by square is in equilibrium with product B represented by circles. Then value of equilibrium constant is
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|


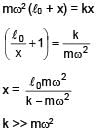
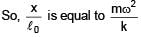
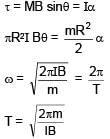
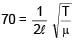
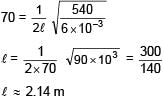
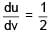 stress x
stress x 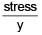
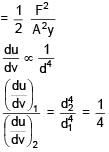
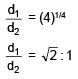

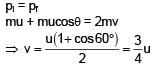
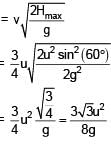

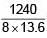 nm
nm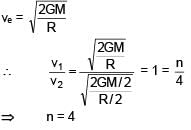
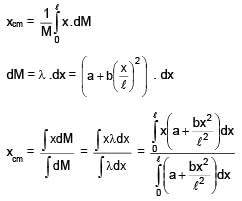
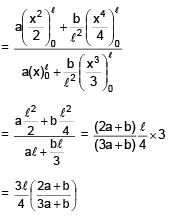
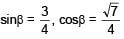
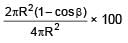
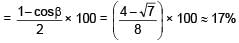


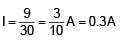
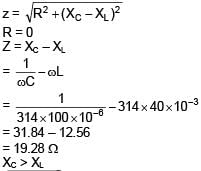
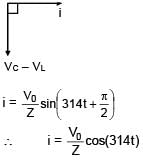
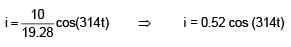
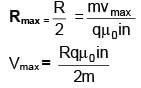
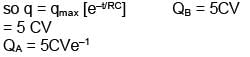
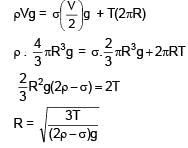
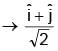
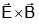 --> direction of propagation of EM wave
--> direction of propagation of EM wave