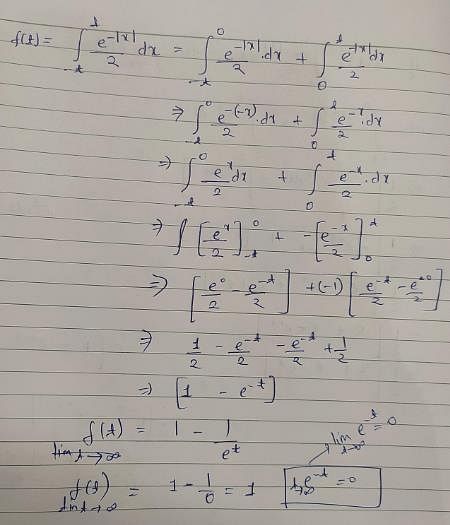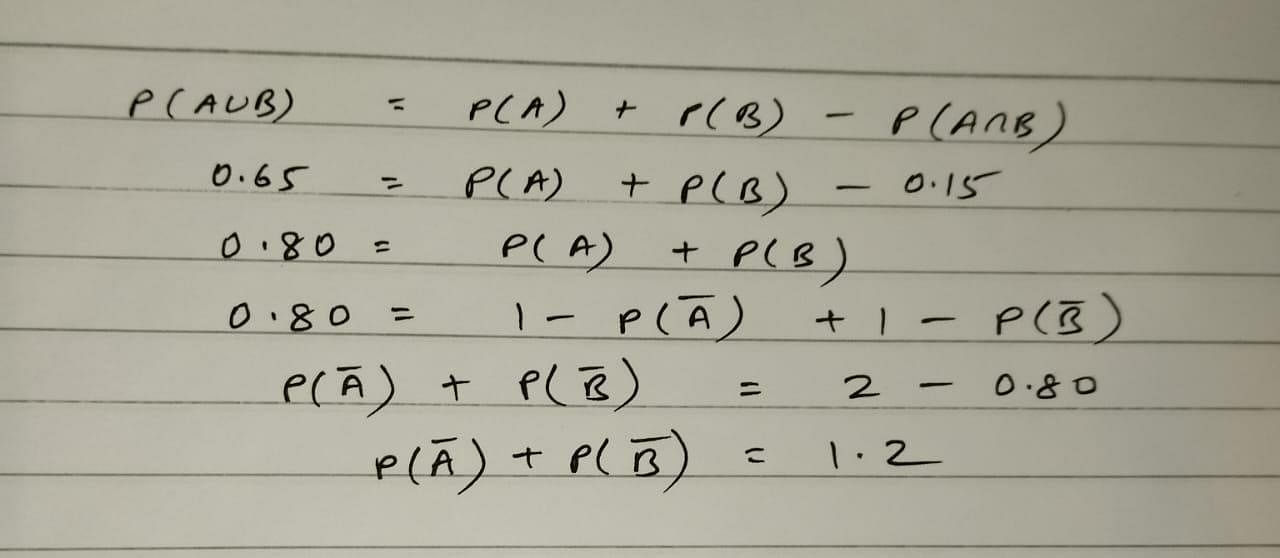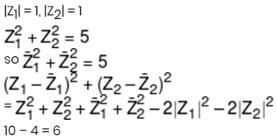All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Mock Tests for JEE Main and Advanced 2025  >  JEE Main Maths Mock Test- 2 - JEE MCQ

JEE Main Maths Mock Test- 2 - JEE MCQ


Test Description

25 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Maths Mock Test- 2

JEE Main Maths Mock Test- 2 for JEE 2024 is part of Mock Tests for JEE Main and Advanced 2025 preparation. The JEE Main Maths Mock Test- 2 questions and answers have been prepared according to the JEE exam syllabus.The JEE Main Maths Mock Test- 2 MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for JEE Main Maths Mock Test- 2 below.
Solutions of JEE Main Maths Mock Test- 2 questions in English are available as part of our Mock Tests for JEE Main and Advanced 2025 for JEE & JEE Main Maths Mock Test- 2 solutions in Hindi for Mock Tests for JEE Main and Advanced 2025 course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt JEE Main Maths Mock Test- 2 | 25 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study Mock Tests for JEE Main and Advanced 2025 for JEE Exam | Download free PDF with solutions
JEE Main Maths Mock Test- 2 - Question 1
Save

The orthocentre of the traingle whose vertices are (5, -2), (-1, 2) and (1,4) is

JEE Main Maths Mock Test- 2 - Question 2
Save

If the equation [(k(x+1)2/3)]+[(y+2)2/4]=1 represents a circle, then k=

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 2
The given equation can be write as


=> 4k(x+1) ²+3(y+2) ²=12

on expanding wee get x² coefficient as 4k
and y² coefficient as 3
but in equation of circle x² coefficient is equal to y² coefficient

therefore 4k=3
=> k=3/4
1 Crore+ students have signed up on EduRev. Have you? Download the App
JEE Main Maths Mock Test- 2 - Question 3
Save

The eccentric angles of the extremities of the latus-rectum intersecting positive x-axis of the ellipse ((x2/a2) + (y2/b2) = 1) are given by

JEE Main Maths Mock Test- 2 - Question 4
Save

If arg (z) = θ, then arg(z̅) =
JEE Main Maths Mock Test- 2 - Question 5
Save

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 5


Hence the answer will be 1.

JEE Main Maths Mock Test- 2 - Question 6
Save

If N N+ denotes the set of all positive integers and if f : NN+ → N is defined by f(n)    = the sum of positive divisors of (n)  then f (2k . 3), where k is a positive integer is
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 6

f(2k. 3) = The sum of positive divisors of 2k . 3 

JEE Main Maths Mock Test- 2 - Question 7
Save

If a, b, c are different and 

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 7

Correct Answer : b

Explanation : A = {(a, a2, a3-1) (b, b2, b3-1) (c, c2, c3-1)}

=> {(a, a2, a3) (b, b2, b3) (c, c2, c3)} - {(a, a2, 1) (b, b2, 1) (c, c2, 1)} = 0

=> abc{(1, a, a2) (1, b, b2) (1, c, c2)} - {(a, a2, 1) (b, b2, 1) (c, c2, 1)} = 0

=> abc{(a, a2, 1) (b, b2, 1) (c, c2, 1)} - {(a, a2, 1) (b, b2 1) (c, c2, 1)} = 0

=> (abc-1){(a, a2, 1) (b, b2, 1) (c, c2, 1)} = 0

abc - 1 = 0

=> abc = 1

JEE Main Maths Mock Test- 2 - Question 8
Save

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 8

JEE Main Maths Mock Test- 2 - Question 9
Save

In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion (A): Angle between is acute angle

Reason (R): If is acute then is obtuse then

JEE Main Maths Mock Test- 2 - Question 10
Save

The point on the curve y = x2 which is nearest to (3, 0) is
JEE Main Maths Mock Test- 2 - Question 11
Save

The degree of the differential equation
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 11

JEE Main Maths Mock Test- 2 - Question 12
Save

In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion (A): are non zero vectors then is a vector perpendicular to all the vectors a → , b → , c →
Reason (R): are perpendicular to both

JEE Main Maths Mock Test- 2 - Question 13
Save

If i2 = -1, then the sum i + i2 + i3 + ..... upto 1000 terms is equal to
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 13
There will equal n opposite signed terms that is 500 +ve one and 500-ve one therefore it's value comes to zero.
JEE Main Maths Mock Test- 2 - Question 14
Save

A parallelogram is cut by two sets of m lines parallel to the sides, the number of parallelogram thus formed is
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 14
Parallelogram is cut by two sets of m parallel lines to its sides.
then we have  2 sets of (m+2) parallel lines ( 2 lines of the parallelogram)
so parallelogram is formed by taking 2 lines from each set
 = m+2C2 * m+2C2
 = [(m+2)(m+1)/2 ]2
 this also include 1 original parallelogram
 so total number of new parallelogram formed is  =  (m + 2)2(m + 1)2/4
JEE Main Maths Mock Test- 2 - Question 15
Save

If A and B are two events such that 
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 15

JEE Main Maths Mock Test- 2 - Question 16
Save

The probability that a leap year will have exactly 52 Tuesdays is
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 16

The probability of a year being a leap year is 1/4 and being non-leap is 3/4.A leap year has 366 days or 52 weeks and 2 odd days. The two odd days can be {Sunday,Monday},{Monday,Tuesday},{Tuesday,Wednesday}, Wednesday,Thursday},{Thursday,Friday},{Friday,Saturday},{Saturday,Sunday}.So there are 7 possibiliyies out of which 2 have a Sunday. So the probability of 53 Sundays in a leap year is 2/7.

So, the probability of 52 sundays is 1-2/7 = 5/7.

JEE Main Maths Mock Test- 2 - Question 17
Save

Product of the real roots of the equation t2x2 + ∣x∣ + 9 = 0
JEE Main Maths Mock Test- 2 - Question 18
Save

If A.M. between two numbers is 5 and their G.M. is 4, then their H.M. is
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 18

If x, y and z respectively represent AM, GM and HM between two numbers a and b, then
y2 = xz
Here x = 5, y = 4
then 16 = 5 x z
z = 16/5

JEE Main Maths Mock Test- 2 - Question 19
Save

If the coefficient of correlation between x and y is 0.28, covariance between x and y is 7.6, and the variance of x is 9, then the standard deviation of the y series is
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 19
N the given problem it is SD of x is 3: (or Variance of x is 9). As Variance = (Sx)^2. We know the relation : correlation coefficient (r) = Cov (x,y) / (Sx * Sy) so, 0.28 = 7.6 / (3 * Sy) From here we get the value of SD of Y : Sy = 9.05.
JEE Main Maths Mock Test- 2 - Question 20
Save

The equation line passing through the point P(1,2) whose portion cut by axes is bisected at P, is
Detailed Solution for JEE Main Maths Mock Test- 2 - Question 20

*Answer can only contain numeric values
JEE Main Maths Mock Test- 2 - Question 21
Save

 

If 2 tan2x – 5 sec x is equal to 1 for exactly 7 distinct values of X ∈ [0, nπ/2], n ∈ N, then the greatest value of n is

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 21

2tan2x – 5sec x = 1
2 (sec2x – 1) – 5secx = 1
2sec2x – 5sec – 3 = 1
∴  cosx = 1/3

*Answer can only contain numeric values
JEE Main Maths Mock Test- 2 - Question 22
Save

If the mean deviation of the number 1, 1 + d, ... , 1 + 8d from their mean is 205, then d is equal to

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 22

*Answer can only contain numeric values
JEE Main Maths Mock Test- 2 - Question 23
Save

The number of 5-digit numbers of the form xyzyx in which x < y is :-

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 23

for z → 10 choice
for  First two x and y → 9C2 choice
Last two y and x → 1 choice
10 × 9C2 × 1= 360

*Answer can only contain numeric values
JEE Main Maths Mock Test- 2 - Question 24
Save

If z1 and z2 are two unimodular complex numbers that satisfy z12 + z22 = 5, then 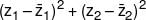 is equal to -

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 24

*Answer can only contain numeric values
JEE Main Maths Mock Test- 2 - Question 25
Save

The AM of 9 term is 15. If one more term is added to this series, then the A.M. becomes 16. The value of added term is :

Detailed Solution for JEE Main Maths Mock Test- 2 - Question 25

Sum of 9 term = 9 × 15 = 135
New sum when Mean is 16
= 16 × 10 = 160
New term = 160 – 135 ⇒ 25

357 docs|148 tests
Join Course
Information about JEE Main Maths Mock Test- 2 Page
In this test you can find the Exam questions for JEE Main Maths Mock Test- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for JEE Main Maths Mock Test- 2, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for JEE Main Maths Mock Test- 2

Find all the important questions for JEE Main Maths Mock Test- 2 at EduRev.Get fully prepared for JEE Main Maths Mock Test- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the JEE Main Maths Mock Test- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of JEE Main Maths Mock Test- 2 resources.

JEE Main Maths Mock Test- 2 MCQs with Answers

Prepare for the JEE Main Maths Mock Test- 2 within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for JEE Main Maths Mock Test- 2 Mock Tests for JEE Main and Advanced 2025

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace JEE Main Maths Mock Test- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily