JEE Main Maths Mock Test- 3 - JEE MCQ
25 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Maths Mock Test- 3
if the pair of lines ax2 + 2hxy + by2 + 2gx + 2fy + c = 0
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The differential equation of the family of lines passing through the origin is
If f: R → R and g : R → R defined by f(x) = 2x + 3 and g(x) = x2 + 7, then the value of x for which f(g(x)) = 25 are
The area bounded by the curve y = x2 - 4x, x-axis and line x = 2 is
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): f (x) = log x3 and g (x) = 3 log x are equal .
Reason(R) : Two functions f and g are said to be equal if their domains, ranges are equal and f (x) = g (x) ∀ x in the domain .
A tangent is drawn at the point (3√3 cos θ, sin θ) 0 < θ < (π/2) of an ellipse (x2/27) + (y2/1) = 1 the least value of the sum of the intercepts on the co-ordinate axes by this tangent is attained at θ =
Which of the following statements are true ?
(1) The amplitude of the product of complex numbers is equal to the product of their amplitudes.
(2) For any polynomial f(x) =0 with real co-efficients, imaginary roots occurs in conjugate paris.
(3) Order relation exists in complex numbers whereas it does not exist in real numbers.
(4) The value of ω used as a cube root of unity and as a fourth root of unity are different.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion (A):
Reason (R): The non zero vectors are always linearly independent
How many numbers between 99 and 1000 can be formed from the digits 2,3,7,0,8,6 so that in each number each digit may occur once only?
The probabilities of solving a problem by three student A,B,C are 1/2, 1/3, 1/4 respectively. The probability that problem will be solved is
If two dice are thrown, find the probability of getting an odd number of on one and multiple of 3 on the other is
If the roots of ax2 + bx + c = 0 are α,β and roots of Ax2 + Bx + C = 0 are α + K, β + K, then B2 - 4AC/b2 - 4ac is equal to
Let f(x) be a polynominal function of second degree,If f(1) = f(-1) and a,b,c are in A.P., then f'(a),f'(b) and f'(c) are in
The total expenditure incurred by an industry under different heads is best presented as a
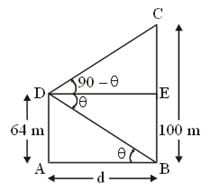
A house of height 100 m subtends a right angle at the window of an opposite house. If the height of the window be 64 m, then the distance between the two houses is
A line makes α/2, β/2, γ/2 angles with positive direction of coordinate axes then cosα + cosβ + cosγ equals-
If a, b and c are perpendicular to b + c, c + a and a + b respectively and if |a + b| = 6, |b + c| = 8 and |c + a| = 10 then |a + b + c| =
|
357 docs|148 tests
|
|
357 docs|148 tests
|





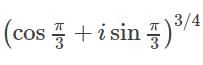 is
is
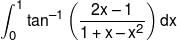 is :-
is :-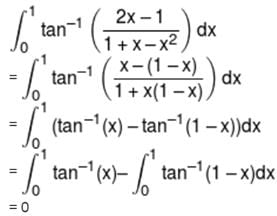
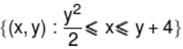 is :-
is :-














