MA Mathematics - 2015 GATE Paper (Practice Test) - GATE MCQ

Tanya is older than Eric.

Cliff is polder than Tanya

Eric is older than cliff.

If the first two statements are true, then the third statement is :

Five teams have to compete in a league, with every team playing every other team exactly once, before going to the next round. How many matches will have to be held to completer the league round of matches?

Q No 6 - 10 carry Two marks each

Q.

Select the appropriate option in place of underlined part of the sentnce.

" Increased productivity necessary " reflects greater efforts made by the employee.

Given below are two statements followed by two conclusions. Assuming these statements to be true, decide which one logically follows.

Statements:

I. No manager is leader.

II All leaders are executives.

Conclusions:

I No manager is an executive

II No executive is a manager.

In the given figure angle  is a right angle, PS:QS= 3:1, RT: QT=5:2 and PU: UR = 1:1. if area of triangle QTS is 20 cm².  then the area of triangle PQR in cm² is ________________.

(Important : you should answer only the numeric value)

Right triangle PQR is to be constructed in the xy- plane so that the right angle is at P and line PR is parallel to the x-axis. The x and y coordinates of P,Q, and R are to be integers that satisfy the inequalities -4x5 and 6 y 16. How many diffrent triangles could be constructed with these properties ?

A coin is tossed thrice. Let X be the event that head occurs in each of the first two tosses. Let Y be the event that a tail occurs on the third toss. Let Z be the event that two tails occur in three tosses. Based on the  above information, which one of the following statements is TRUE?

Q. 11 – Q. 35 carry one mark each.

Q.

Let T : R⁴ → R⁴ be a linear map defined by

Then the rank of T is equal to _________

(Important : you should answer only the numeric value)

Let M be a 3 x 3 matrix and suppose that 1, 2 and 3 are the eigenvalues of M. If

for some scalar α 0, then α is equal to ___________

(Important : you should answer only the numeric value)

Let M be a 3 x 3 singular matrix and suppose that 2 and 3 are eigenvalues of M. Then the number
of linearly independent eigenvectors of M₃ + 2 M +I₃  is equal to _________

(Important : you should answer only the numeric value)

Let M be a 3 x 3 matrix such that   and suppose that  for
some . Then | α| is equal to _______

(Important : you should answer only the numeric value)

Let be defined by 

         Then the function f is

Consider the power series 

The radius of convergence of the series is equal to __________

(Important : you should answer only the numeric value)

Let C={zC : |z-i|=2} . then  is equal to ____________

(Important : you should answer only the numeric value)

Let   is equal to ___________

(Important : you should answer only the numeric value)

Let the random variable X have the distribution function

Then P(2X<4) is equal to ___________

(Important : you should answer only the numeric value)

Let X be a random variable having the distribution function

Then E(X) is equal to _________

(Important : you should answer only the numeric value)

In an experiment, a fair die is rolled until two sixes are obtained in succession. The probability that
the experiment will end in the fifth trial is equal to

Let x₁ = 2.2, x₂ = 4.3, x₃ = 3.1, x₄ = 4.5, x₅ = 1.1 and x₆ = 5.7 be the observed values of a
random sample of size 6 from a U(θ - 1, θ + 4) distribution, where θ ∈ (0, ∞) is unknown. Then
a maximum likelihood estimate of θ is equal to

Let  be the open unit disc in  with boundary is the solution of the Dirichlet problem

then u(1/2,0) is equal to

Let c ∈ Z₃ be such that  is a field. Then c is equal to __________

(Important : you should answer only the numeric value)
 

Let  Then V is

Let  be defined by  is equal to __________

(Important : you should answer only the numeric value)

Let 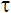₁be the usual topology on R. Let 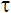₂ be the topology on R generated by

Let X be a connected topological space such that there exists a non-constant continuous function
f : X → R, where R is equipped with the usual topology. Let f(X) = { f(x): x ∈ X}. Then

Let d₁ and d₂ denote the usual metric and the discrete metric on R, respectively. Let  be defined by f(x) = x, x ∈ R. Then

If the trapezoidal rule with single interval [0, 1] is exact for approximating the integral 

then the value of c is equal to ________

(Important : you should answer only the numeric value)