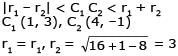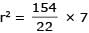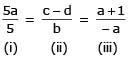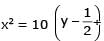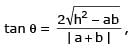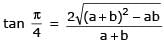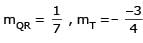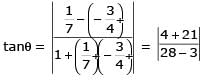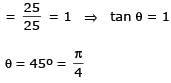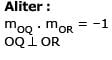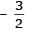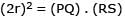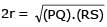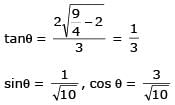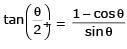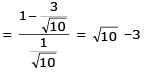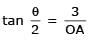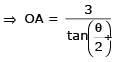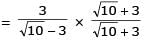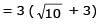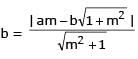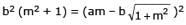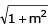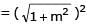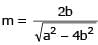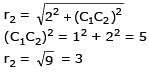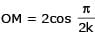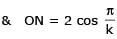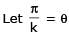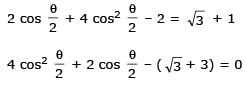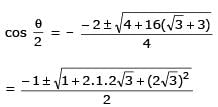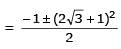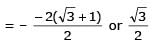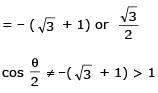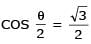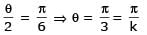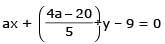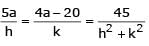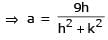MCQ (Previous Year Questions) - Circle (Competition Level 1) - JEE MCQ
24 Questions MCQ Test Additional Study Material for JEE - MCQ (Previous Year Questions) - Circle (Competition Level 1)
The square of the length of tangent from (3, –4) on the circle x2 + y2 – 4x – 6y + 3 = 0
[AIEEE-2002]
If the two circles (x – 1)2 + (y – 3)2 = r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then
[AIEEE-2003]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle having area as 154 sq. units. Then the equation of the circle is
[AIEEE-2003]
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = 4 orthogonally, then the locus of its centre is
-[AIEEE-2004]
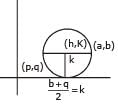
A variable circle passes through the fixed point A(p, q) and touches x-axis. The locus of the other end of the diameter through A is -
[AIEEE-2004]
If the lines 2x + 3y + 1 = 0 and 3x – y – 4 = 0 lie along diameters of a circle of circumference 10π, then the equation of the circle is -
[AIEEE-2004]
If the circles x2 + y2 + 2ax + cy + a = 0 and x2 + y2 – 3ax + dy – 1 = 0 intersect in two distinct point P and Q then the lines 5x + by – a = 0 passes through P and Q for -
[AIEEE-2005]
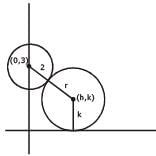
A circle touches the x-axis and also touches the circle with centre at (0, 3) and radius 2. The locus of the centre of the circle is -
[AIEEE-2005]
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = p2 orthogonally, then the equation of the locus of its centre is -
[AIEEE-2005]
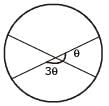
If the pair of line ax2 + 2(a + b)xy + by2 = 0 lie along diameters of a circle and divide the circle into four sectors such that the area of one of the sectors is thrice the area of another sector then
[AIEEE-2005]
If thel ines 3x – 4y – 7 = 0 and 2x – 3y – 5 = 0 are two diameters of a circle of area 49 π square units, the equation of the circle is -
[AIEEE-2006]
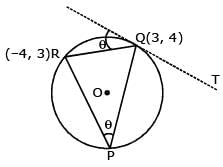
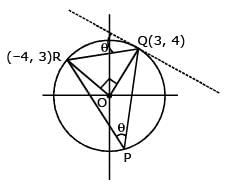
The triangle PQR is inscribed in the circle, x2+y2 = 25. If Q and R have co-ordinates (3, 4) & (–4, 3) respectively, then √QPR is equal to
[JEE 2000(Scr.), 1 + 1]
If the circles, x2 + y2 + 2x + 2ky + 6 = 0 & x2 + y2 + 2ky + k = 0 intersect orthogonally, then ‘k’ is
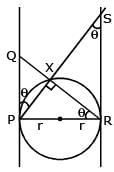
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle then 2r equals.
[JEE 2001 (Scr.), 1]
Let 2x2 + y2 – 3xy = 0 be the equation of a pair of tangents drawn from the origin 'O' to a circle of radius 3 with centre in the first quadrant. If A is one of the points of contact, find the length of OA.
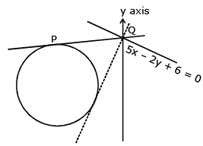
If the tangent at the point P on the circle x2 + y2 + 6x +6y = 2 meets the straight line 5x – 2y + 6 = 0 at a point Q on the y-axis, then the length of PQ is
If a > 2b > 0 then the positive value of m for which i s a common tangent to x2 + y2 = b2 and (x - a)2 + y2 = b2 is
[JEE 2002 (Scr.)]
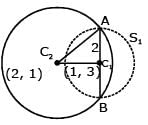
The radius of the circle, having centre at (2, 1), whose one of the chord is a diameter of the circle x2 + y2 – 2x – 6y + 6 = 0
[JEE 2004(Scr.)]
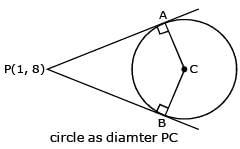
Tangents drawn from the point P(1, 8) to the circle x2 + y2 – 6x – 4y – 11 = 0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
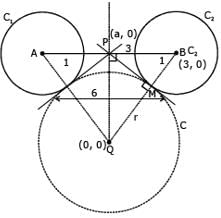
The centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2 and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C is
[JEE 2009]
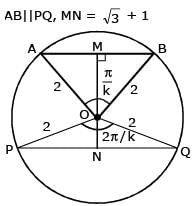
Two parallel chords of a circle of radius 2 are at a distance 3 + 1 apart. If the chords subtend at the center, angles of π/k andk 2π/k , where k > 0, then the value of [k] is
{Note : [k] denotes the largest integer less than or equal to k}
[JEE 2010]
The circle passing through the point (–1, 0) and touching the y-axis at (0, 2) also passes through the point
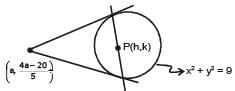
The locus of the mid-point of the chord of contact of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is
[JEE 2012]
A tangent PT is drawn to the circle x2 + y2 = 4 at the point P (√3, 1) . A straight line L, perpendicular toPT is a tangent to the circle (x – 3)2 + y2 = 1. A possible equation of L is
[JEE 2012]
|
22 videos|162 docs|17 tests
|
|
22 videos|162 docs|17 tests
|