MCQ (Previous Year Questions) - Complex Numbers (Competition Level 2) - JEE MCQ
13 Questions MCQ Test - MCQ (Previous Year Questions) - Complex Numbers (Competition Level 2)
If a, b are the roots of the equation, (x – a)(x – b) + c = 0, find the roots of the equation, (x – a)(x – b) = c. [REE 2000 (Mains), 3]
(a) For the equation, 3x2 + px + 3 = 0, p > 0 if one of the roots is square of the other, then p is equal to
(A) 1/3 (B) 1 (C) 3 (D) 2/3
(b) If a & b (a < b), are the roots of the equation, x2 + bx + c = 0, where c < 0 < b, then
(A) 0 < a < b (B) a < 0 < b < | a | (C) a < b < 0 (D) a < 0 < | a | < b
(c) If b > a, then the equation, (x – a) (x – b) – 1 = 0, has
(A) both roots in [a, b] (B) both roots in (-∞, a)
(C) both roots in [b, ∞) (D) one root in (–∞, a) & other in (b, + ∞)
(d) If a, b are the roots of ax2 + bx + c = 0, (a ¹ 0) and a + d, b + d, are the roots of Ax2 + Bx + C = 0, (A ¹ 0) for some constant d, then prove that, 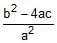 =
= 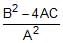 . [JEE 2000(Mains), 4]
. [JEE 2000(Mains), 4]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let a, b, c be real numbers with a ¹ 0 and let a, b be the roots of the equation ax2 + bx + c = 0. Express the roots of a3x2 + abcx + c3 = 0 in terms of a, b. [JEE 2001(Mains), 5]
The set of all real numbers x for which x2 – |x + 2| + x > 0, is [JEE 2002 (Scr.), 3]
If x2 + (a – b)x + (1 – a – b) = 0 where a, b ∈ R then find the values of `a' for which equation has unequal real roots for all values of `b'. [JEE 2003 (Mains), 4]
(a) If one root of the equation x2 + px + q = 0 is the square of the other, then [JEE 2004 (Scr.)]
(A) p3+q2–q(3p+1)=0 (B) p3+q2 + q(1+3p)=0 (C) p3+q2+q(3p_1)=0 (D) p3+q2+q(1–3p)=0
(b) If x2 + 2ax + 10 _ 3a > 0 for all x Î R, then
(A) –5 < a < 2 (B) a < –5 (C) a > 5 (D) 2 < a < 5
If |z1| = 4, |z2| = 4, then |z1 + z2 + 3 + 4i| is less than
(a) Let a, b, c be the sides of a triangle. No two of them are equal and λ ∈ R. If the roots of the equation x2 + 2(a + b + c)x + 3λ(ab + bc + ca) = 0 are real, then [JEE 2006, 3 + 6]
(A) l < (B) l >
(C) l <
(D) l <
(b) If roots of the equation x2 –10cx –11d = 0 are a, b and those of x2 – 10ax – 11b = 0 are c, d, then find the values of a + b + c + d. (a, b, c and d are distinct numbers)
(a) Let a, b be the roots of the equation
x2 – px + r = 0 and a/2, 2b be the roots of the equation x2 – qx + r = 0. Then the value of `r' is
[JEE 2007, 3 + 6]
(A) (p – q)(2q – p) (B)
(q – p)(2p – q) (C)
(q – 2p)(2q – p) (D)
(2p – q)(2q – p)
(b) Let f(x) =
Match the expressions / statements in Column I with expressions / statements in Column II.
Column–I Column–II
(A) If –1 < x < 1, then f(x) satisfies (P) 0 < f(x) < 1
(B) If 1 < x < 2, the f(x) satisfies (Q) f(x) < 0
(C) If 3 < x < 5, then f(x) satisfies (R) f(x) > 0
(D) If x > 5, then f(x) satisfies (S) f(x) < 1
Let a, b, c, p, q be real numbers. Suppose a, b are the roots of the equation x2 + 2px + q = 0 and a, 1/b are the roots of the equation ax2 + 2bx + c = 0, where b2 Ï {_1, 0, 1} [JEE 2008, 3]
statement–1 : (p2 – q)(b2 – ac) ³ 0
statement–2 : b ¹ pa or c ¹ qa
Let p and q are real numbers such that p ¹ q, p3 ¹ q and p3 ¹ _q. If a and b are two non zero complex number satisfies a + b = –p and a3 + b3 = q then quadratic equation whose roots are and
, is
Let a and b be the roots of x2 – 6x – 2 = 0, with a > b. If an = an – bn for n > 1, then the value of is
A value of b for which the equations x2 + bx – 1 = 0, x2 + x + b = 0, have one root in common is

















