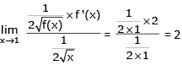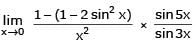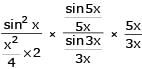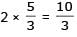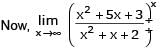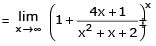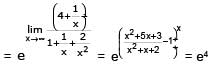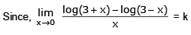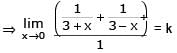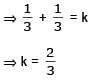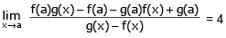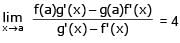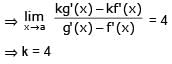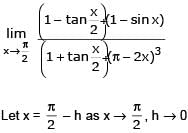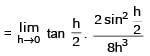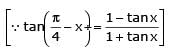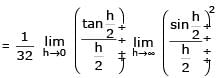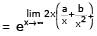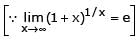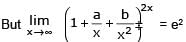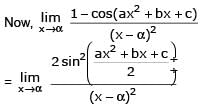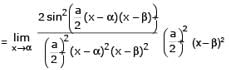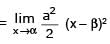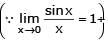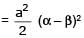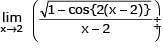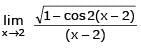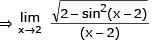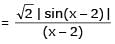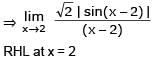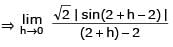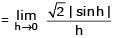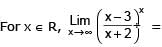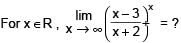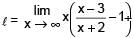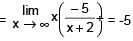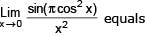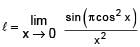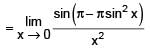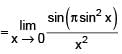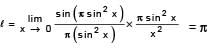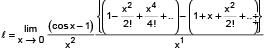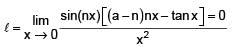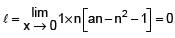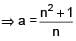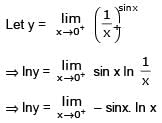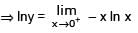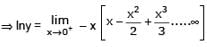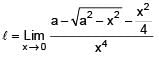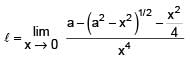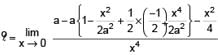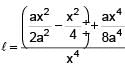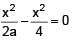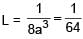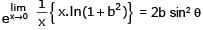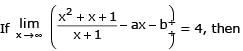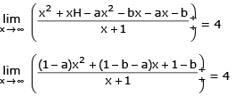MCQ (Previous Year Questions) - Limit (Competition Level 1) - JEE MCQ
Test Description
18 Questions MCQ Test - MCQ (Previous Year Questions) - Limit (Competition Level 1)
MCQ (Previous Year Questions) - Limit (Competition Level 1) for JEE 2024 is part of JEE preparation. The MCQ (Previous Year Questions) - Limit (Competition Level 1) questions and answers have been prepared
according to the JEE exam syllabus.The MCQ (Previous Year Questions) - Limit (Competition Level 1) MCQs are made for JEE 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ (Previous Year Questions) - Limit (Competition Level 1) below.
Solutions of MCQ (Previous Year Questions) - Limit (Competition Level 1) questions in English are available as part of our course for JEE & MCQ (Previous Year Questions) - Limit (Competition Level 1) solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt MCQ (Previous Year Questions) - Limit (Competition Level 1) | 18 questions in 18 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 1
If f(1) = 1, f' (1) = 2, then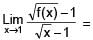 
[AIEEE 2002]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 1
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 2
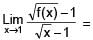
The value of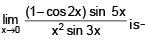 
[AIEEE 2002]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 3
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 4
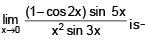
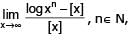(where [x] denotes greatest integer less than or equal to x)
[AIEEE-2002]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 4
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 5
If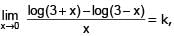 
the value of k is -
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 5
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 6
Let f(a) = g(a) = k and their nth derivatives f n (a), gn(a) exist and are not equal for some n. Further if 
then the value of k is-
[AIEEE 2003]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 6
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 7
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 8
then the values of a and b, are-
[AIEEE 2004]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 8
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 9
Let α and β be the distinct roots of ax2 + bx + c = 0, then 
is equal to -
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 9
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 10
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 11
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 12
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 13
The integer n for which 
is a finite non-zero number is
[JEE 2002 (Scr.)]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 13
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 14
If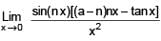 
= 0 (n > 0)then the value of ‘a’ is equal to
[JEE 2003 (Scr.)]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 14
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 15
For x > 0,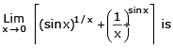 
[JEE 2006, 3]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 15
*Multiple options can be correct
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 16
Let L =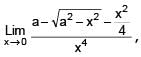 
a > 0, If L is finite, then
[JEE 2009, 4]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 16
MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 17
If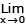 
[1 + x In (1+b2)]1/x = 2b sin2 θ, b > 0 and θ ∈ (-π, π]. Then the value of θ is
[JEE 2011, 3]
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 17
Detailed Solution for MCQ (Previous Year Questions) - Limit (Competition Level 1) - Question 18
Information about MCQ (Previous Year Questions) - Limit (Competition Level 1) Page
In this test you can find the Exam questions for MCQ (Previous Year Questions) - Limit (Competition Level 1) solved & explained in the simplest way possible.
Besides giving Questions and answers for MCQ (Previous Year Questions) - Limit (Competition Level 1), EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for JEE
Important Questions for MCQ (Previous Year Questions) - Limit (Competition Level 1)
Find all the important questions for MCQ (Previous Year Questions) - Limit (Competition Level 1) at EduRev.Get fully prepared for MCQ (Previous Year Questions) - Limit (Competition Level 1) with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the MCQ (Previous Year Questions) - Limit (Competition Level 1) syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of MCQ (Previous Year Questions) - Limit (Competition Level 1) resources.
MCQ (Previous Year Questions) - Limit (Competition Level 1)
Prepare for the MCQ (Previous Year Questions) - Limit (Competition Level 1) within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for MCQ (Previous Year Questions) - Limit (Competition Level 1)
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ (Previous Year Questions) - Limit (Competition Level 1) with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup