MCQ (Previous Year Questions) - Triangle (Competition Level 1) - JEE MCQ
22 Questions MCQ Test - MCQ (Previous Year Questions) - Triangle (Competition Level 1)
The sum of the radii of inscribed and circumscribed circles for an n sided regular polygon of side a, is -
[AIEEE 2003]
If in a triangle ABC a cos2 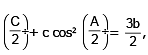 then the sides a, b and c
then the sides a, b and c
[AIEEE 2003]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a triangle ABC, medians AD and BE are drawn. In AD = 4, ∠ DAB = π/6 and ∠ABE = π/3 , then the area of the ΔABC is-
[AIEEE 2003]
The sides of a triangle are sin α, cos α and for some
Then the greatest angle of the triangle is-
In a triangle ABC, let ∠c = π/2 If r is the in-radius and R is the circumradius of the triangle ABC, then 2(r + R) equals -
[AIEEE-2005]
For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is -
[AIEEE-2010]
ABCD is a trapezium such that AB and CD are parallel and , BC = p and CD = q, then AB is equal to :
[JEE-MAIN 2013]
The radii r1, r2, r3 of escribed circles of a triangle ABC are in harmonic progression. If its area is 24 sq. cm and its perimeter is 24 cm, find the lengths of its sides.
[REE 99, 6]
(a) In a triangle ABC, Let ∠C = π/2 . If 'r' is the inradius and 'R' is the circumradius of the triangle, then 2(r + R) is equal to [JEE 2000 (Scr.), 1 + 1]
(b) In a triangle ABC, 2 ac sin 1/2 (A – B + C) =
Which of the following pieces of data does NOT uniquely determine an acute-angled triangle ABC (R being the radius of the circumcircle) ?
[JEE 2002 (Scr.), 3]
The ratio of the sides of a triangle ABC is 1 : √3 : 2. The ratio A : B : C is
[JEE 2004, (Scr.)]
In ΔABC, a, b, c are the lengths of its sides and A, B, C are the angles of triangle ABC. The correct relation is
Circles with radii 3, 4 and 5 touch each other externally if P is the point of intersection of tangents to these circles at their points of contact. Find the distance of P from the points of contact.
[JEE 2005 (Mains)]
Given an isosceles triangle, whose one angle is 120º and radius of its incircle is √3 . Then the area of triangle in sq. units is
[JEE 2006, 3]
Internal bisector of ∠A of a triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent side of ΔABC then
[JEE 2006, 5]
Let ABC and ABC' be two non-congruent triangles with sides AB = 4, AC = AC' = 2 2 and angle B = 30º. The absolute value of the difference between the areas of these triangles is
[JEE 2009, 5]
In a triangle ABC with fixed base BC, the vertex A moves such that cosB + cosC = 4 sin 2A/2. If a, b and c denote the lengths of the sides of the triangle opposite to the angles A, B and C, respectively, then
[JEE 2009]
If the angles A, B and C of a triangle are in an arithmetic progression and if a, b and c denote the lengths of the sides opposite to A, B and C respectively, then the value of the expression
Let ABC be a triangle such that ∠ACB = π/6 and let a, b and c denote the lengths of the sides opposite to A, B and C respectively. The value(s) of x for which a = x2 + x + 1, b = x2 – 1 and c = 2x + 1 is (are)
Consider a triangle ABC and let a, b and c denote the lengths of the sides opposite to vertices A, B and C respectively. Suppose a = 6, b = 10 and the area of t he t riang l e i s 15 √3 . If ∠ACB is obtuse and if r denotes the radius of the incircle of the triangle, then r2 is equal to
[JEE 2010]
Let PQR be a triangle of area D with a = 2, b =7/2 and c =5/2 where a, b and c are the lengths of the sides of the triangle opposite to the angles at P, Q and R respectively. Then

















