MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - JEE MCQ
Test Description
10 Questions MCQ Test - MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2)
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) for JEE 2024 is part of JEE preparation. The MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) questions and answers have been prepared
according to the JEE exam syllabus.The MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) MCQs are made for JEE 2024 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) below.
Solutions of MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) questions in English are available as part of our course for JEE & MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) | 10 questions in 10 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 1
Find real values of x for which, 27cos 2x . 81sin 2x is minimum. Also find this minimum value. [REE 2000, 3]
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 2
Solve the following system of equation for x and y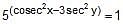 
and 
. [REE 2001 (mains), 3]
and 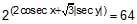. [REE 2001 (mains), 3]| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 3
The number of integral values of k for which the equation 7 cos x + 5 sin x = 2k + 1 has a solution is [JEE 2002 (Screening), 3]
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 4
cos(a – b) = 1 and cos(a + b) = 1/e, where a, b Î [–p, p], number of pairs of a, b which satisfy both the equations is [JEE 2005 (Screening)]
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 5
If 0 < q < 2p, then the intervals of values of q for which 2 sin2q – 5sinq + 2 > 0, is [JEE 2006, 3]
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 6
The number of solutions of the pair of equations 2sin2q – cos 2q = 0 and 2cos2 q – 3 sin q = 0 in the interval [0, 2p] is [JEE 2007, 3]
*Multiple options can be correct
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 7
For 0 < q < p/2, then solution(s) of 
(q + (m –1)p/4) cosec(q + mp/4) = 4
is(are) [JEE 2009]
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 8
The number of values of q in the interval 
such that 
for n=0, ±1, ±2 and tanq = cot 5q as well as sin2q = cos4q is [JEE 2010]
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 9
The number of all possible values of q when qÎ(0, p) for which the system of equation [JEE 2010]
(y + z) cos 3q = (xyz) sin 3q
x sin3q = 
(xyz) sin 3q = (y + 2z)cos 3q + y sin 3q have a solution (x0, y0, z0) with y0,z0 ¹ 0 is
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) - Question 10
Let P = {q : sin q – cos q = 
cos q} and Q = {q : sin q + cos q = 
sin q} be two sets. Then [JEE 2011]
Information about MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) Page
In this test you can find the Exam questions for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) solved & explained in the simplest way possible.
Besides giving Questions and answers for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2), EduRev gives you an ample number of Online tests for practice
Download as PDF
Top Courses for JEE
Important Questions for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2)
Find all the important questions for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) at EduRev.Get fully prepared for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) with EduRev's comprehensive question bank and test resources.
Our platform offers a diverse range of question papers covering various topics within the MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) syllabus.
Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered.
The questions are designed to challenge you and help you gain confidence in tackling the actual exam.
Maximize your chances of success by utilizing EduRev's extensive collection of MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) resources.
MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2)
Prepare for the MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) within the JEE exam with comprehensive MCQs and answers at EduRev.
Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus.
Access the best books, study materials, and notes curated by toppers to enhance your preparation.
Stay updated with the exam date and receive expert preparation tips and paper analysis.
Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.
Online Tests for MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2)
Practice with a wide array of question papers that follow the exam pattern and syllabus.
Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement.
Access detailed solutions and explanations for each test to enhance your understanding of concepts.
With EduRev's Online Tests, you can build confidence, boost your performance, and ace MCQ (Previous Year Questions) - Trigonometric Equations (Competition Level 2) with ease.
Join thousands of successful students who have benefited from our trusted online resources.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup