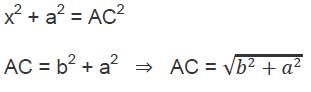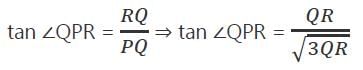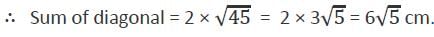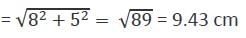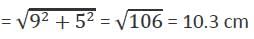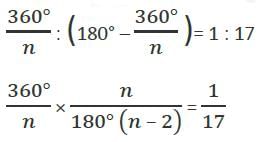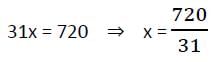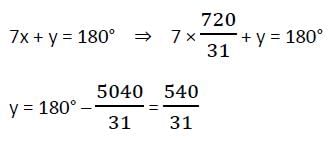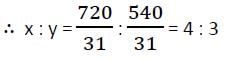MCQ: Quadrilaterals and Polygons - 1 - SSC CGL MCQ
15 Questions MCQ Test - MCQ: Quadrilaterals and Polygons - 1
Directions: Kindly study the following questions carefully and choose the right answer:
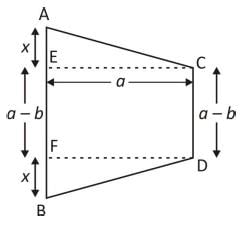
Two light rods AB = a + b, CD = a – b symmetrically lying on a horizontal AB. There are kept intact by two strings AC and BD. The perpendicular distance between rods in a. The length of AC is given by
Directions: Kindly study the following questions carefully and choose the right answer:
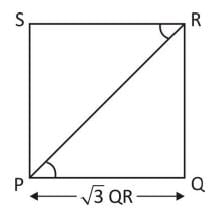
If PQRS be a rectangle such PQ = √3 QR. Then, what is ? PRS equal to ?
Directions: Kindly study the following questions carefully and choose the right answer:
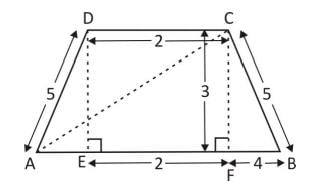
In a trapezium, the two non-parallel sides are equal in length, each being of 5 cm. The parallel sides are at a distance of 3 cm apart. If the smaller side of the parallel sides is of length 2 cm, then the sum of the diagonals of the trapezium is
Directions: Kindly study the following questions carefully and choose the right answer:
The area of a rectangle lies between 40 cm2 and 45 cm2. If one of the sides is 5 cm, then its diagonal lies between
Directions: Kindly study the following questions carefully and choose the right answer:
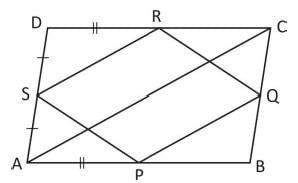
Let ABCD be a parallelogram. Let P, Q, R and S be the mid-points of sides AB,
BC, CD and DA respectively. Consider the following statements.
I. Area of triangle APS < Area of triangle DSR, if BD < AC.
II. Area of triangle ABC = 4 (Area of triangle BPQ).
Select the correct answer using the codes given below.
Directions: Kindly study the following Questions carefully and choose the right answer:
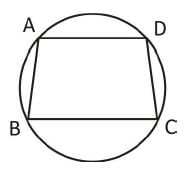
ABCD is a cyclic trapezium such that AD || BC, if ∠ABC = 70°, then the value of ∠BCD is :
Directions: Kindly study the following Questions carefully and choose the right answer:
ABCD is a cyclic trapezium such that AD || BC, if ∠ABC = 70°, then the value of ∠BCD is :
Directions: Kindly study the following Questions carefully and choose the right answer:
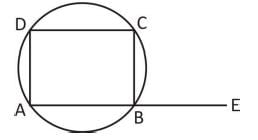
If an exterior angle of a cyclic quadrilateral be 50°, then the interior opposite angles is :
Directions: Kindly study the following Questions carefully and choose the right answer:
ABCD is a cyclic quadrilateral and O is the centre of the circle. If ∠COD = 140° and ∠BAC = 40°, then the value of ∠BCD is equal to
Directions: Kindly study the following Questions carefully and choose the right answer:
If the ratio of an external angle and an internal angle of a regular polygon is 1 :17, then the number of sides of the regular polygon is
Directions: Kindly study the following questions carefully and choose the right answer:
In a cyclic quadrilateral ∠A + ∠C = ∠B + ∠D = ?
Directions: Kindly study the following questions carefully and choose the right answer:
If ABCD be a cyclic quadrilateral in which ∠A = 4x°, ∠B = 7x°, ∠C = 5y°, ∠D = y°, then x : y is
Directions: Kindly study the following questions carefully and choose the right answer:
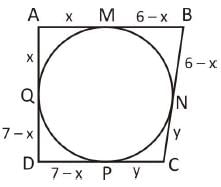
A quadrilateral ABCD circumscribes a circle and AB = 6 cm, CD = 5 cm and AD =7 cm. The length of side BC is
Directions: Kindly study the following questions carefully and choose the right answer:
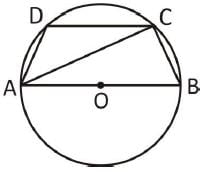
ABCD is a cyclic quadrilateral and AB is a diameter. If ∠BAC = 55° then value of ∠ADC is
Directions: Kindly study the following questions carefully and choose the right answer:
The difference between the exterior and interior angles at a vertex of a regular polygon is 150°. The number of sides of the polygon is