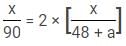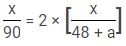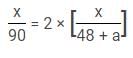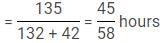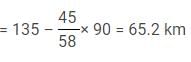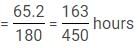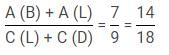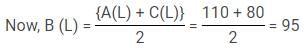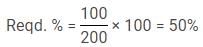MCQ Test: Caselets - 2 - Banking Exams MCQ
20 Questions MCQ Test - MCQ Test: Caselets - 2
Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Q. What should come in place of A?
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Q. What should come in place of C?
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Q. What will come in place of B?
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Directions: Study the following information carefully and answer the questions given beside.
Two trains A and B running at speeds 42 km/hr and 48 km/hr respectively are approaching each other. They are [A] km far from each other. After 12 minutes, a vulture starts flying from train A towards train B at the speed of [B] km/hr. It reverses its direction as soon as it reached B and starts filying towards A and continues this until trains A and B meet. The total distance covered by it is [C] km. The vulture meets train B (first time) in half the time train A meets train B (from the time vulture started). The distance between the points where train B meets vulture for the first time and train B meets train A is 72 km. The distance between trains A and B, when the vulture meets train B for the second time is [D].
Q. What should come in place of D?
Directions: Study the following information carefully and answer the questions given beside.
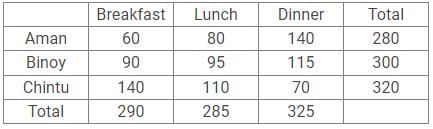
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.
The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.
Q. What is the ratio of amount spent by Aman on breakfast and dinner to the amount spent by Chintu on breakfast and dinner?
Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.
The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.
Q. What is the difference between the total amount spent on breakfast and dinner?
Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.
The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.
Q. What would have been the ratio of total amount spent by Aman and Binoy, had they split the dinner amount paid by Chintu between them evenly?
Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.
The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.
Q. The amount spent on dinner by Binoy is what percent of the total amount spent by him?
Directions: Study the following information carefully and answer the questions given beside.
Aman, Binoy and Chintu are three friends who go out to explore the city. They ate their breakfast, lunch and dinner in the market and split the total bill. The amount spent by Aman on breakfast and lunch is in the ratio 3 : 4, while that spent by Chintu on lunch and dinner is in the ratio 11 : 7.
The amount paid by Aman on Dinner and Chintu on breakfast is equal. In lunch, the share of Binoy is the average of Aman and Chintu. The money spent by Aman on Breakfast and lunch is 700/9% of the money spent by Chintu on lunch and dinner. The ratio of breakfast, lunch and dinner in the total bill is 58 : 57 : 65. In the end Aman gives Chintu Rs. 20, to make the share of each of them equal.
Q. The amount spent by Aman on breakfast, Binoy on lunch and Chintu on dinner is what percent of the total expenditure of all three?
Directions: Study the following information carefully and answer the questions given beside.
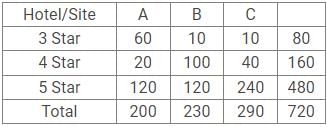
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website.
Further it is known that
- Total number of hotels listed on all three website together is 720.
- Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together.
- Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
- Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
- Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
- Number of 3 star hotels on website B and C are same.
Q. 4 Star Hotels on Site B is what percent of total number Hotels on Site A ?
Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website.
Further it is known that
- Total number of hotels listed on all three website together is 720.
- Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together.
- Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
- Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
- Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
- Number of 3 star hotels on website B and C are same.
Q. What is the total number of 4 star hotels from website A and C together ?
Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website.
Further it is known that
- Total number of hotels listed on all three website together is 720.
- Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together.
- Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
- Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
- Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
- Number of 3 star hotels on website B and C are same.
Q. Website D also started listing of Hotels on their site. Number of 3 star hotels on site D is 50% more than number of 4 star hotels on site A. Total number of hotels (3 star, 4 star and 5 star) on site D are 500, out of which 50% are 4 star. Find the number of 5 star hotels listed on site D.
Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website.
Further it is known that
- Total number of hotels listed on all three website together is 720.
- Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together.
- Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
- Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
- Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
- Number of 3 star hotels on website B and C are same.
Q. What is the difference between 3 star hotels on site A and 4 star hotels on site C ?
Directions: Study the following information carefully and answer the questions given beside.
Three online hotel booking website A,B and C listed some hotels on their websites. The all listed 3 star, 4 star and 5 star hotels. One hotel can be listed on exactly one website.
Further it is known that
- Total number of hotels listed on all three website together is 720.
- Total number of 4 star hotels is twice the total number of 3 star hotels on all the three websites taken together. Further, total number of 5 star hotels is thrice the total number of 4 star hotels on all three sites together.
- Out of 200 hotels listed on Websites A, 30% are 3 star hotels.
- Ratio of 5 star hotels on sites A,B and C are 1 : 1 : 2.
- Number of 5 star hotels on B website is 20% more than number of 4 star hotels on the same website.
- Number of 3 star hotels on website B and C are same.
Q. What is the total number of Hotels listed on Website C ?
Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.
Q. How much did the bank have to pay in total for two years on behalf of Natasha?
Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.
Q. Find, the annual amount spent on utilities is what percentage less than the annual amount spent on rent? (Approximate)
Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.
Q. Natasha decides to live with her relatives for 6 months so she will not have to pay for rent and utilities. How much does she save on rent and utilities?
Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.
Q. If the bank charges simple interest at the rate of 9% per annum, then find the total interest amount that Natasha paid after 2 years. (Assume she pays off the entire loan after 2 years of completion of course)
Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.
Q. Natasha gets an internship for a period of 3 months. The company where she'll be doing internship pays $12000 per month. The utilities and rent for these 3 months is what percentage of the total amount she earns from the internship?
Direction: Read the following information carefully and answer the questions given below it.
Natasha wants to pursue her B. Tech from Massachusetts Institute of Technology, United States, but to be able to afford it, she has to take an education loan. The loan agreement guaranteed to pay 80% of all her expenses. This way she only had to bear the remaining costs. As soon as she landed in the United States, she had to pay the rent for her new apartment. The apartment rent was $550 per month. She then paid her tuition fee for the current semester worth $25000. On an average she spent $340 on utilities and groceries per month. Given that, Natasha's course lasted a total of two years (comprising of 2 semesters per year) and the bank gave 80% of the total expenses of two years at the beginning of her course.
Q. How much money did Natasha have to bear for her two-year course at MIT, considering the loan agreement guaranteed to pay 80% of all her expenses?