MCQ Test: Experimental Probability - 2 - Bank Exams MCQ
20 Questions MCQ Test - MCQ Test: Experimental Probability - 2
Three dice are thrown. What is the probability that each face shows only multiples of 3?
A natural number n is chosen from the first 50 natural numbers. What is the probability that 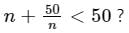
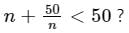
A coin is flipped 100 times, and it lands heads-up 63 times. What is the experimental probability of getting tails?
A spinner is divided into 6 equal sections, numbered from 1 to 6. If the spinner is spun 200 times, and the number 3 comes up 45 times, what is the experimental probability of landing on 3?
In a deck of 52 playing cards, 10 cards are red (hearts and diamonds). If 25 cards are drawn randomly, what is the experimental probability of drawing a red card?
A bag contains 15 green marbles and 25 blue marbles. If three marbles are drawn randomly, what is the experimental probability of drawing a green marble?
A six-sided die is rolled 120 times, and the number 4 comes up 30 times. What is the experimental probability of rolling a 4?
A box contains 12 red balls and 8 blue balls. If two balls are drawn randomly without replacement, what is the experimental probability of drawing a red ball followed by a blue ball?
A box contains 25 chocolates: 10 are milk chocolate, 8 are dark chocolate, and the rest are white chocolate. If one chocolate is drawn randomly, what is the experimental probability of drawing a white chocolate?
A bag contains 6 red balls and 4 green balls. If three balls are drawn randomly with replacement, what is the experimental probability of drawing exactly two red balls?
A spinner is divided into 8 equal sections, numbered from 1 to 8. If the spinner is spun 160 times, and the number 7 comes up 40 times, what is the experimental probability of landing on a number greater than 4?
A box contains 30 marbles: 18 are red, and 12 are blue. If two marbles are drawn randomly without replacement, what is the experimental probability of drawing two blue marbles?
A bag contains 5 red balls, 4 green balls, and 6 blue balls. If three balls are drawn randomly with replacement, what is the experimental probability of drawing exactly two red balls?
A fair six-sided die is rolled 50 times. If the number 2 comes up 10 times, what is the experimental probability of not rolling a 2?
In a box, there are 8 red balls and 12 blue balls. If two balls are drawn randomly with replacement, what is the experimental probability of drawing two red balls?
In a class of 30 students, 15 students play football, 10 students play basketball, and the rest play cricket. If one student is chosen randomly, what is the experimental probability of selecting a student who plays cricket?
A bag contains 7 red balls and 3 blue balls. If three balls are drawn randomly with replacement, what is the experimental probability of drawing exactly two blue balls?
A box contains 5 white balls, 4 black balls, and 6 red balls. If two balls are drawn randomly without replacement, what is the experimental probability of drawing a black ball followed by a red ball?
A six-sided die is rolled 200 times, and the number 6 comes up 25 times. What is the experimental probability of rolling a number other than 6?
A bag contains 8 yellow balls and 12 green balls. If two balls are drawn randomly with replacement, what is the experimental probability of drawing a yellow ball and a green ball?


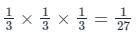
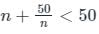 would be
would be











