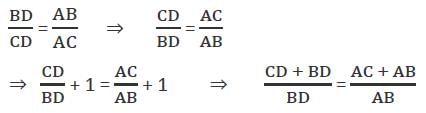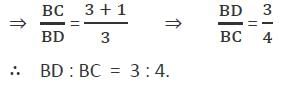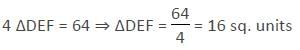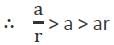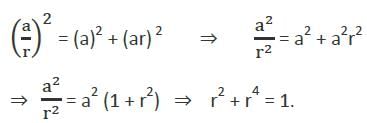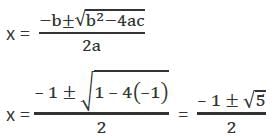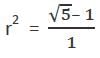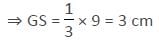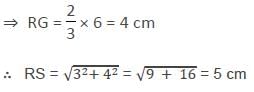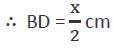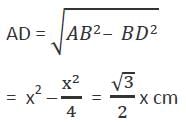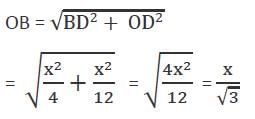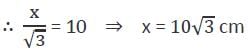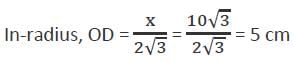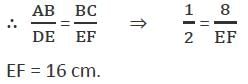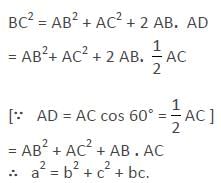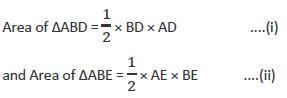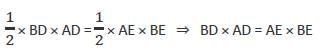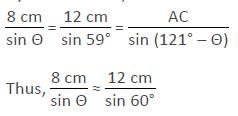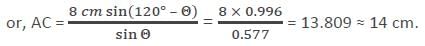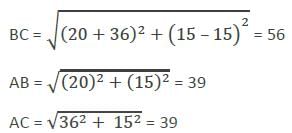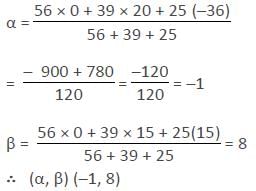MCQ: Triangles - 2 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Triangles - 2
Directions: Study the following question carefully and choose the right answer:
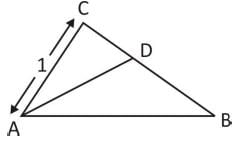
If AD is the internal angular bisector of angle A of ΔABC with AB = 3 cm and AC= 1 cm, then what is BD : BC equal to?
Directions: Study the following question carefully and choose the right answer:
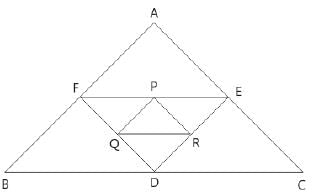
In the above figure, if area of triangle ABC is 64 sq. units, then find the area of triangle PQR, where D, E and F are mid points of sides of ΔABC and P, Q and R are midpoints of sides of ΔDEF.

Directions: Study the following question carefully and choose the right answer:
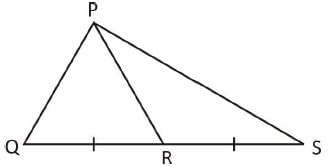
The side QR of an equilateral triangle PQR is produced to the point S in such a way that QR = RS and P is joined to S. Then the measure of ∠ PSR is
The side QR of an equilateral triangle PQR is produced to the point S in such a way that QR = RS and P is joined to S. Then the measure of ∠ PSR is
Directions: Study the following question carefully and choose the right answer:
The sides of a triangle are in geometric progression with common ratio r < 1. If the triangle is a right angled triangle, the square of common ratio is given by
Directions: Study the following question carefully and choose the right answer:
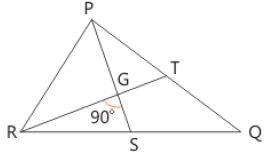
Two medians PS and RT of ΔPQR intersect at G at right angles. If PS = 9 cm and RT = 6 cm,then the length of RS in cm is
Directions: Study the following question carefully and choose the right answer:
If the circumradius of an equilateral triangle be 10 cm, then the measure of its in-radius is
Directions: Study the following question carefully and choose the right answer:
If triangles ABC and DEF are similar such that 2AB = DE and BC = 8 cm, then what is EF equal to?
Directions: Study the following question carefully and choose the right answer:
In the adjoining figure, if BC = a, AC = b, AB = c and ∠CAB = 120° , then the correct relation is :

Directions: Kindly study the following Question carefully and choose the right answer:
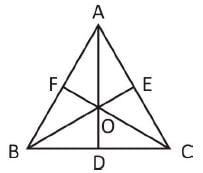
If the incentre of an equilateral triangle lies inside the triangle and its radius is 3 cm, then the side of the equilateral triangle is
Directions: Kindly study the following Question carefully and choose the right answer:
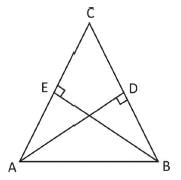
In a ΔABC, AD is perpendicular to BC and BE is perpendicular to AC. Which of the following is correct?
Directions: Kindly study the following Question carefully and choose the right answer:
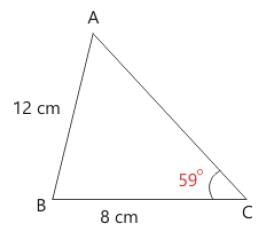
The length of side AB and side BC of a scalene triangle ABC are 12 cm and 8 cm respectively. The value of angle C is 59°. Find the length of side AC.
Directions: Kindly study the following Question carefully and choose the right answer:
In a triangle, if orthocentre, circumcentre, incentre and centroid coincide, then the triangle must be
Directions: Kindly study the following Question carefully and choose the right answer:
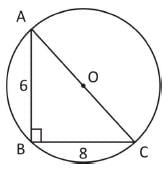
Let ABC is triangle right angled at B. If AB = 6 cm and BC = 8 cm, then what is the length of the circumradius of the ΔABC?
Directions: Study the following question carefully and choose the right answer:
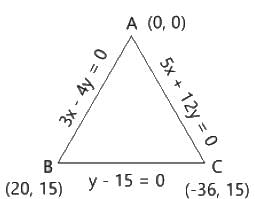
The coordinates of the in centre of the triangle whose sides are 3x – 4y = 0, 5x + 12y = 0 and y – 15 = 0, are
Directions: Study the following question carefully and choose the right answer:
If ABC is an equilateral triangle and P, Q, R respectively denote the middle points of AB, BC, CA then.
|
342 videos|301 docs|185 tests
|