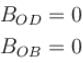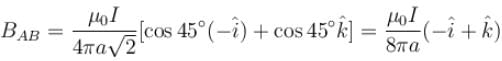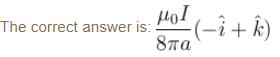Magnetic Effect Of Current MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Magnetic Effect Of Current MCQ Level - 2
Determine the magnetic field at the centre of the current carrying wire arrangement shown in the figure. The arrangement extends to infinity. (The wires joining the successive squares are along the line passing through the centre)
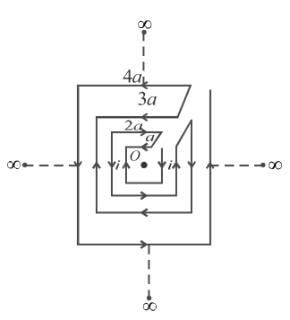

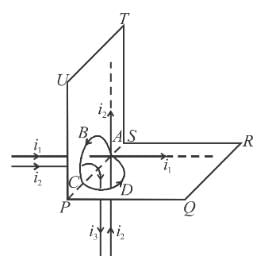
Figure shows an amperian path ABCDA. Part ABC is in vertical plane PSTU while part CDA is in horizontal plane PQRS. Direction of circulation along the path is shown by an arrow near point B and at D. 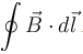 for this path according to Ampere’s law will be :
for this path according to Ampere’s law will be :
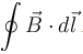 for this path according to Ampere’s law will be :
for this path according to Ampere’s law will be :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
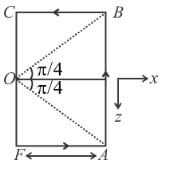
In the figure shown A B C D E F A was a square loop of side l, but is folded in two equal parts so that half of it lies in x z plane and the other half lies in the i'. The magnetic field at the centre is :


A particle is moving with velocity 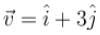 and it produces an electric field at a point given by
and it produces an electric field at a point given by 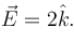 It will produce magnetic field at that point equal to (all quantities are S.I. units)
It will produce magnetic field at that point equal to (all quantities are S.I. units)
A ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is :
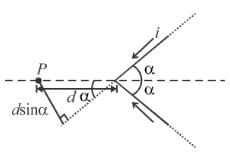
If the magnetic field at ‘P’ in the given figure can be written as  then K is:
then K is:
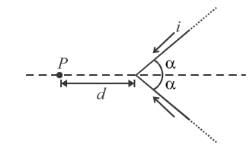
Two infinitely long linear conductors are arranged perpendicular to each other and are in mutually perpendicular planes as shown in figure. If I1 = 2A along the y-axis and I2 = 3A along negative z-axis and AP = AB = 1cm. The value of magnetic field strength 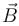 at P is -
at P is -

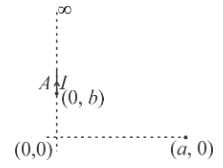
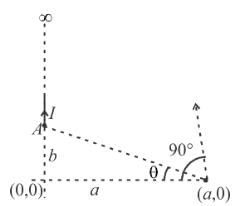
An infinitely long wire carrying current I is along Y axis such that its one end is at point A(0, b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a, 0) is.
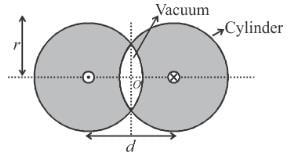
Two long cylinders (with axis parallel) are arranged as shown to form overlapping cylinders, each of radius r, whose centers are separated by a distance d. Current of density J (Current per unit area) flows into the plane of page along the right shaded part of one cylinder and an equal current flows out of the plane of the page along the left shaded part of the other, as shown in the figure. The magnitude and direction of magnetic field at point O (O is the origin of shown x-y axes) are :
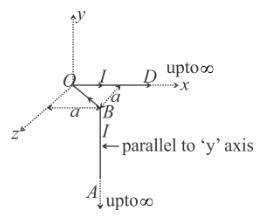
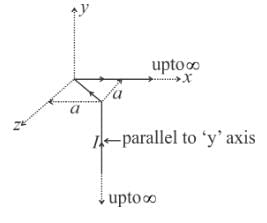
The magnetic field at the origin due to the current flowing in the wire as shown in figure below is :


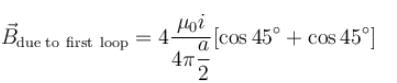
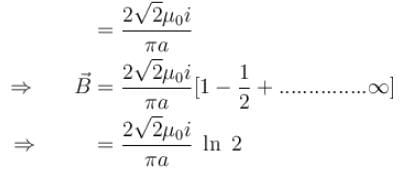
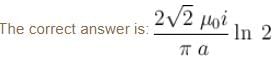


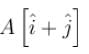
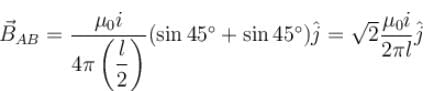 Due to BC :
Due to BC :
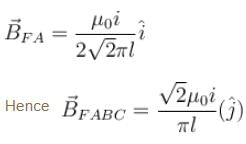

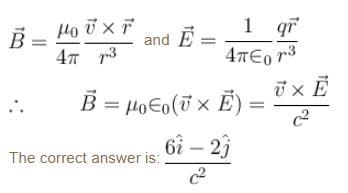
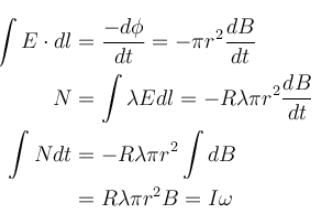
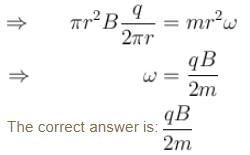

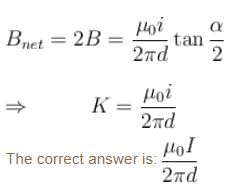
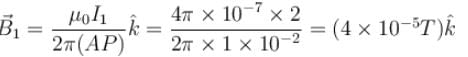
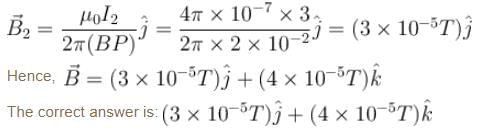
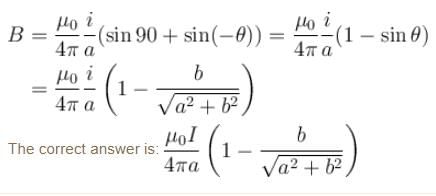
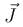 , then current density in complete right cylinder is
, then current density in complete right cylinder is 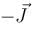 . Then magnetic field at any point P in the region of overlap is
. Then magnetic field at any point P in the region of overlap is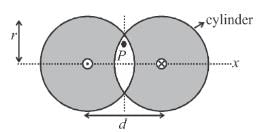
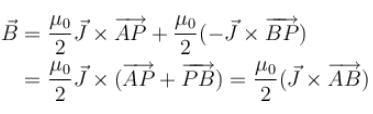
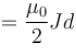 and its direction is along positive y-direction at any point P in overlap region.
and its direction is along positive y-direction at any point P in overlap region.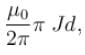 in the + y -direction
in the + y -direction