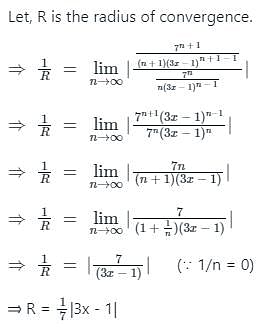Math - 2014 Past Year Paper - IIT JAM MCQ

For a, b, c ∈ R, if the differential equation (ax² + bxy + y²)dx + (2x² + cxy + y²)dy = 0 is exact, then

If f(x, y, z) = x²y + y²z + z²x for all (x, y, z) ∈ R³ and     then the value of

at (1, 1, 1) is

Let G be a group of order 17. The total number of non- isomorphic subgroups of G is

Which one of the following is a subspace of the vector space R³ ?

Let T : R³ →  R³ be the linear transformation defined by T(x, y, z) = (x + y, y + z, z + x) for all (x, y, z) ∈ R³. Then

Let f:  R → R be a continuous function satisfying   for all x ∈ R . Then the set 

  is the interval

Directions: Q.11 – Q.35 carry two marks each.

The system of linear equations

x – y + 2z = b₁

x + 2y – z = b₂

2y – 2z = b₃
is inconsistent when (b₁, b₂, b₃) equals

  be a matrix with real entries. If the sum and the product of all the eigenvalues
of A are 10 30 respectively, then a² + b² equals

Consider the subspace W = {(x₁, x₂, ..., x₁₀) ∈ R¹⁰ : x _n = x_n–1 + x_n–2 for 3 ≤  n ≤ 10} of the vector space R¹⁰. The dimension of W is

Let y₁(x) and y₂(x) be two linearly independent solutions of the differential equation

x₂ y”(x) – 2xy’(x) – 4y(x) = 0 for x ∈ [1, 10].

Consider the Wronskian W(x) = y₁(x)y₂’(x) – y₂(x)y₁’(x). If W(1) = 1, then W(3) – W(2) equals

The equation of the curve passing through the point ,(π/2, 1) and having slope   at each
point (x, y) with x ≠ 0 is

The value of α ∈ R for which the curves x² + αy² = 1 and y = x² intersect orthogonally is

Let {x_n} be a sequence of real numbers such that    where c is a positive real number. Then then sequence {x_n /n} is 

where    Then

The set all limit points of the set 

Let S = [0, 1] ∪  [2, 3) and let f : S → R be defined by 

If T = {f(x) : x ∈ S}, then the inverse function f^–1 : T → S

Let f(x) = x³ + x and g(x) = x³ – x for all x ∈ R. If f^–1 denotes the inverse function of f, then the derivative of the composite function g o f^–1 at the point 2 is

For all (x, y) ∈ R² , 

Then at the point (0, 0),

For all (x, y)  ∈ R² 

Let f : R →  R be a function with continuous derivative such that f ( √2 ) = 2 and f(x) = 

for all x ∈ R. Then f(3) equals

The value of   is 

If C is a smooth curve in R³ from (–1, 0, 1) to (1, 1, –1), then the value of

  is

Let C be the boundary of the region R = {(x, y) ∈ R² : –1 ≤ y ≤ 1, 0 ≤ x ≤ 1 – y²} oriented in the counterclockwise direction. Then the value of  

Let G be a cyclic group of order 24. The total number of group isomorphism’s of G onto itself is