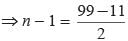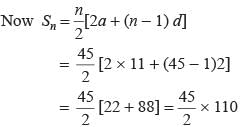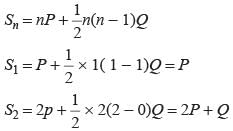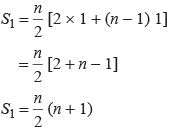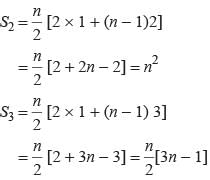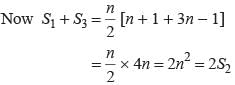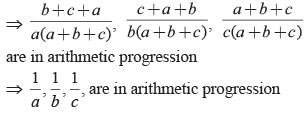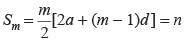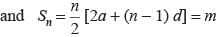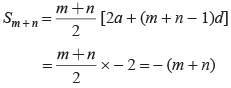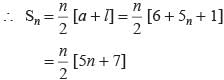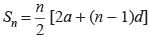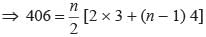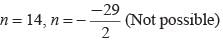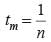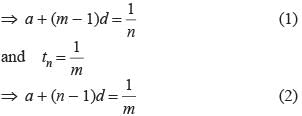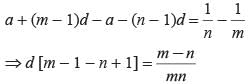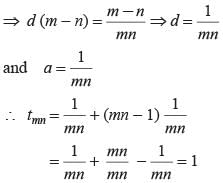Math Olympiad Test: Arithmetic Progression- 2 - Class 10 MCQ
15 Questions MCQ Test - Math Olympiad Test: Arithmetic Progression- 2
Find the sum of all two-digits odd positive integers.
What is the nth term of the sequence log a, log ab, log ab2, log ab3, . . .
If the sum of n terms of an arithmetic progression is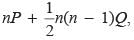 where P and Q are constants. What is the common difference?
where P and Q are constants. What is the common difference?
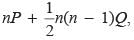 where P and Q are constants. What is the common difference?
where P and Q are constants. What is the common difference?The sum of n terms of the three arithmetic progression are S1, S2, S3. The first term of each arithmetic progression is unity. The common differences are 1, 2, 3 respectively, then which of the following options is correct?
The sum of three numbers in arithmetic is 27 and their product is 405. What are the numbers?
If 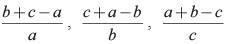 are in arithmetic progression then which of the following is correct?
are in arithmetic progression then which of the following is correct?
What is the sum of all three digit natural numbers which are multiples of 7?
The sum of first seven terms of an arithmetic progression is 10 and the sum of next seven terms is 17, then what is the common difference of this arithmetic progression?
If in an arithmetic progression the sum of m terms is n and the sum of n terms is m then what is the sum of (m + n) terms?
If pth, qth and rth terms of an arithmetic progression are a, b, c respectively, then what is the value of a(q - r) + b(r - p) + c(p - q)?
Find the sum of n terms of an arithmetic progression whose kth term is 5k + 1
How many terms of an arithmetic progression 3, 7, 11, 15, …. are taken so that the sum is 406?
What is the value of k for which 5k + 2, 4k - 1 and k + 2 are in arithmetic progression?
If the mth term of an arithmetic is 1/n and its nth term 1/m then what is its (mn)th term?
The first, second and last term of an arithmetic progression are respectively 4, 7 and 31. How many terms are there in the given arithmetic progression?