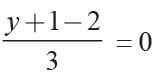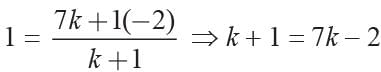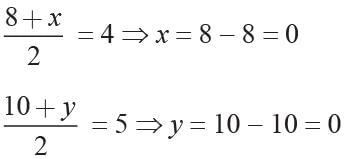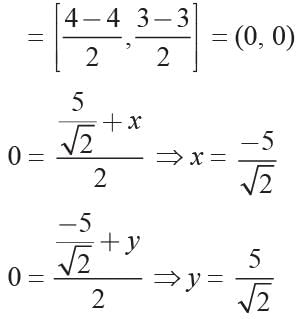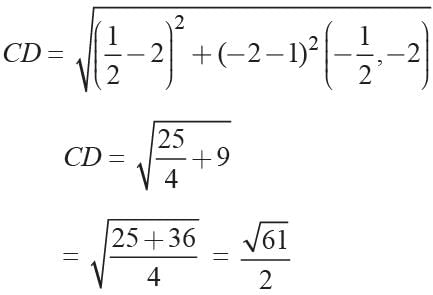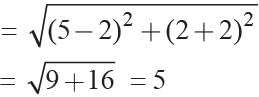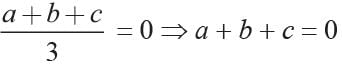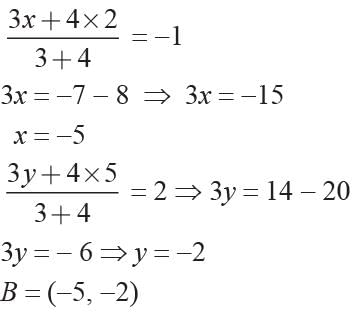Math Olympiad Test: Coordinate Geometry- 2 - Class 10 MCQ
15 Questions MCQ Test - Math Olympiad Test: Coordinate Geometry- 2
Find the third vertex of a ΔABC if two of its vertices are B (-3, 1), C (0, -2), and its centroid is at the origin.
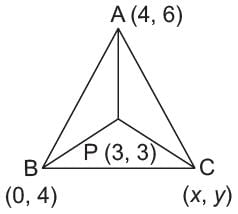
The circumcentre of a triangle is (3, 3). If its two vertices are (4, 6) and (0, 4) find the third vertex of the triangle.
In which ratio does the point P (1, 2) divides the join of A (-2, 1) and B (7, 4)?
If (2, -2), (-2, 1) and (5, 2) are vertices of a right angled triangle, then the area of triangle is
The centre of a circle is (4, 5) A(8, 10) is a point on the circumference. Find the other end of diameter of the circle through A.
The ends of a diameter of a circle have the coordinates (4, 3) and (-4, -3), PQ is another diameter where P has co-ordinate
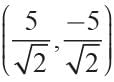
find the coordinates of Q.
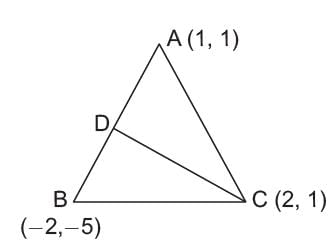
The vertices of a triangle are A(1, 1), B(-2, -5) and C(2, 2) find the length of the medium through C.
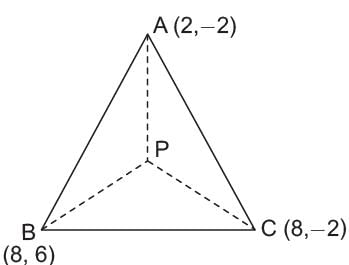
What is the circumradius of the triangle whose vertices are (2, -2), (8, 6), and (8, -2)?
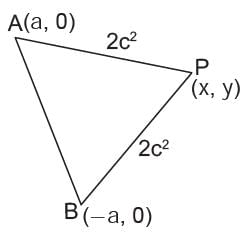
The sum of the square of the distance of a moving point from two fixed points (a, 0) and (-a, 0) is equal to the constant quantity 2c2. Find the equation of its locus.
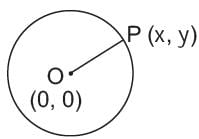
What is the distance of the point (4, 7) from the y-axis?
If the distance between the points (3, 0) and (0, y) is 5 units. y is positive then what is value of y?
If the centroid of the triangle is formed by points P(a, b), Q(b, c) and R(c, a) is at the origin. What is the value of a + b +c?
If the point P(-1, 2) divides externally the line segment joining A(2, 5) and B in the ratio 3 : 4. What is the co-ordinate of point B?
The points A(3, 1), B(0, 4), C(-3, 1), D(0, -2) are vertices of a
If the point (x, 4) lies on a circle whose center is at the origin and radius is 5, What is the value of x?


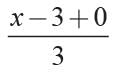 = 0 ⇒ x = 3 and
= 0 ⇒ x = 3 and