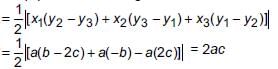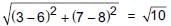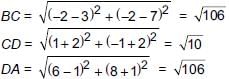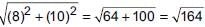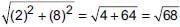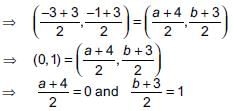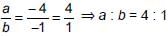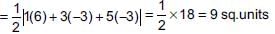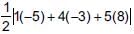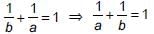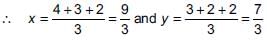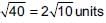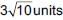Math Olympiad Test: Coordinate Geometry- 3 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Coordinate Geometry- 3
Find the area (i n square units) of the triangle whose vertices are (a, b + c), (a, b – c) and (–a, c).
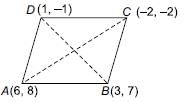
Points (6, 8), (3, 7), (–2, –2) and (1, –1) are joined to form a quadrilateral. What will be the structure of quadrilateral?
Four vertices of a parallelogram taken in order are (–3, –1), (a, b), (3, 3) and (4, 3). What will be the ratio of a and b?
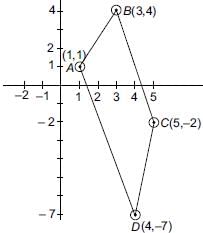
Find the area of the quadrilateral, the coordinates of whose angular points taken in order are (1, 1), (3, 4), (5, –2) and (4, –7).
If the points (a, 0), (0, b) and (1, 1) are collinear then which of the following is true?
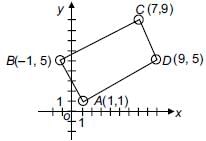
The points (1, 1), (–1, 5), (7, 9) and (9, 5) taken in such order that it will form a
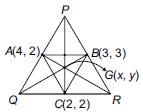
The coordinates of the mid-points of the sides of a triangle are (4, 2), (3, 3) and (2, 2). What will be the coordinates of the centroid of the triangle?
Three points A(1, –2), B(3, 4) and C(4, 7) form
Find the area of triangle whose vertices are (t, t – 2), (t + 2, t + 2) and (t + 3, t).
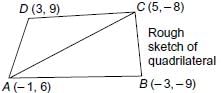
Area of quadrilateral formed by the vertices (–1, 6), (–3, –9), (5, –8) and (3, 9) is _______ (sq. units).