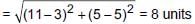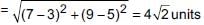Math Olympiad Test: Coordinate Geometry- 4 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Coordinate Geometry- 4
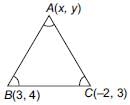
The coordinates of the third vertex of an equilateral triangle whose two vertices are at (3, 4), (–2, 3) are ________.
The vertices of a ΔABC are A(2,1), B(6, –2), C(8, 9). If AD is angle bisector, where D meets on BC, then coordinates of D are _______.
Find the coordinates of the point on X-axis which are equidistant from the points (–3, 4) and (2, 5).
In what ratio is the line segment joining the points (–3, 2) and (6, 1) is divided by Y-axis?
Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in km. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines)
If the centroid of the triangle formed by the points (a, b), (b, c) and (c, a) is at the origin, then a3 + b3 + c3 =
DIRECTION: Students of a school are standing in rows and columns in their playground for drill practice. A, B, C and D are the position of the four students as shown in the figure.
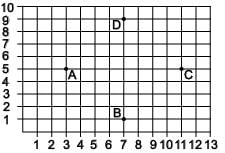
Q. If Mohit wants to stand in such a way that he is equidistance from each of the four students A, B, C and D then what are the coordinate of his position?
DIRECTION: Students of a school are standing in rows and columns in their playground for drill practice. A, B, C and D are the position of the four students as shown in the figure.
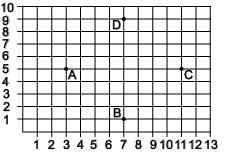
Q. What is the difference of distance between AC and AD?
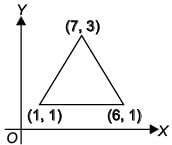
To raise social awareness about t he hazards of smoking, a school decided to start “No smoking campaign”. A student is asked to prepare a campaign banner in the shape of a triangle shown in the figure. If cost of 1 cm2 of banner is ₹2, find the cost of the banner.
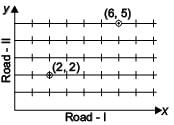
A well planned locality, has two straight roads perpendicular to each other. There are 5 lanes parallel to Road - I. Each lane has 8 houses as seen in figure. Chaitanya lives in the 6th house of the 5th lane and Hamida lives in the 2nd house of the 2nd lane. What will be the shortest distance between their houses?


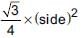
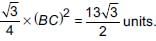
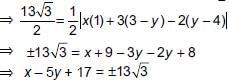
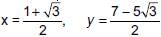

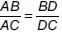 ...(i)
...(i) 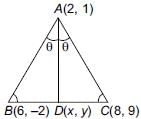
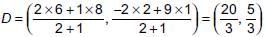

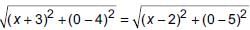

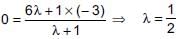
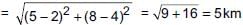
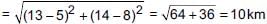
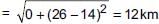
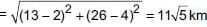
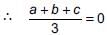 ⇒ a + b + c = 0 ...(i)
⇒ a + b + c = 0 ...(i)