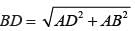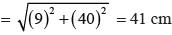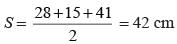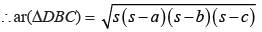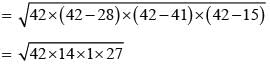Math Olympiad Test: Heron’s Formula- 1 - Class 9 MCQ
10 Questions MCQ Test - Math Olympiad Test: Heron’s Formula- 1
The area of a triangle, whose two sides are 8 cm and 11cm and the perimeter is 32 cm, will be:
If the length of each side of a triangle is multiplied by 3, then the % increase in area will be:
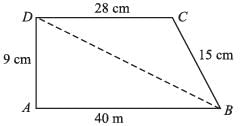
The sides of a triangle are 11cm, 15cm and 16 cm. The altitude to the largest side is:
The length of median of an equilateral triangle is √3 cm. The area of triangle is:
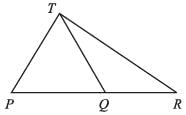
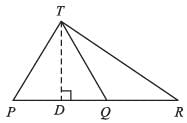
In the figure, PQ : QR = 3 : 2. If the area of ∆PRT = 40 cm2, then area of ∆TQR is:
The area of an equilateral triangle with side 2√3 cm is
If a square and equilateral triangle have same perimeter and, square has area A1 and equilateral triangle has area A2, then
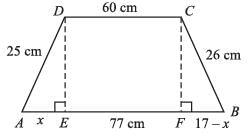
Two parallel sides of a trapezium are 60 cm and 77 cm and other sides are 25 cm and 26 cm. The area of the trapezium is
The area of rhombus whose perimeter is 80m and one of the diagonal is 24m.


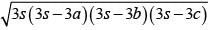
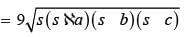
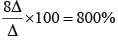

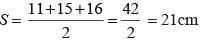
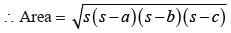
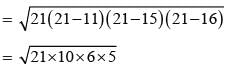
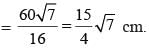
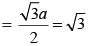
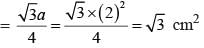

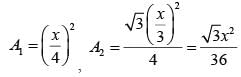 Clearly, A1 > A2
Clearly, A1 > A2