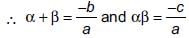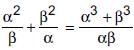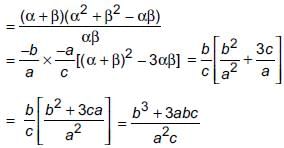Math Olympiad Test: Polynomials - 4 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Polynomials - 4
A polynomial of the form ax5 + bx3 + cx2 + dx + e has atmost _______ zeroes.
If one zero of the polynomial f (x) = (k2 + 4) x2 + 13x + 4k is reciprocal of the other, then k is equal to _______.
For x2 + 2x + 5 to be a factor of x4 + αx2 + β, the values of α and β should respectively be _______.
If α and β are the roots of the equation 2x2 – 7x + 8 = 0, then the equation whose roots are(3α – 4β) and (3β – 4α) is _______.
Area of a triangular field is (x4 – 6x3 – 26x2 + 138x – 35) m2 and base of the triangular field is (x2 – 4x + 1) m. Find the height of the triangular field.
If α, β be two zeroes of the quadratic polynomial ax2 + bx – c = 0, then find the value of 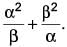
Raghav had ₹(6x3 + 2x2 + 3x) and he bought (4x2 + 3) shirts. The price of each shirt is ₹(x + 5). How much money is left with Raghav?
A rectangular garden of length (2x3 + 5x2 – 7) m has the perimeter (4x3 – 2x2 + 4) m. Find the breadth of the garden.
Length and breadth of a rectangular park are (3x2 + 2x) m and (2x3 – 3) m respectively. Find the area of the park, when x = 3.
Two different container contains (2x3 + 2x2 + 3x + 3) L and (4x3 – 2x2 + 6x – 3) L water. What is biggest measure that can measure both quantities exactly?


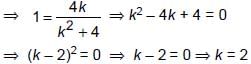


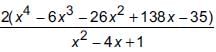

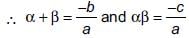 2 + bx – c = 0
2 + bx – c = 0