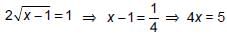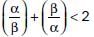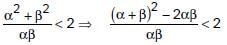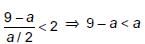Math Olympiad Test: Quadratic Equations- 3 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Quadratic Equations- 3
The roots of ax2 + bx + c = 0, a ≠ 0 are real and unequal, if b2 – 4ac is _______.
If one root of the equation a ( b – c ) x2 + b(c – a)x + c(a – b) = 0 is 1, then the other root is ___.
If 2 is a root of the equation x2 + bx + 12 = 0 and the equation x2 + bx + q = 0 has equal roots, then q is equal to
One of the two students, while solving a quadratic equation in x, copied the constant term incorrectly and got the roots 3 and 2. The other copied the constant term and coefficient of x2 correctly as –6 and 1 respectively. The correct roots are ____.
If the roots of the equation (a – b)x2 + (b – c)x + (c – a) = 0 are equal. Then _______.
If one of roots of 2x2 + ax + 32 = 0 is twice the other root, then the value of a is ________.
Roots of the quadratic equation x2 + x – (a + 1)(a + 2) = 0 are ________.
For what value of a, the roots of t he equation 2x2 + 6x + a = 0, satisfy the condition 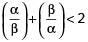 (where α and β are the roots of equation).
(where α and β are the roots of equation).


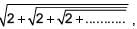 then _______.
then _______.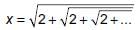 ...(i)
...(i)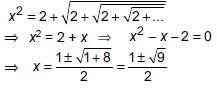
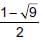


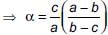
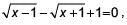 then 4x is equal to ________.
then 4x is equal to ________.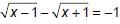 ...(1)
...(1)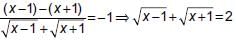 ...(2)
...(2)