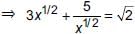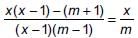Math Olympiad Test: Quadratic Equations- 4 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Quadratic Equations- 4
If the roots of the equation (a2 + b2) x2 – 2b(a + c)x + (b2 + c2) = 0 are equal, then ________.
The roots of the equation 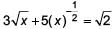 can be found by solving ________.
can be found by solving ________.
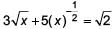 can be found by solving ________.
can be found by solving ________. The roots of the equation x2/3 + x1/3 – 2 = 0 are ________.
Two numbers whose sum is 12 and the absolute value of whose difference is 4 are the roots of the equation ________.
In a bangle shop, if the shopkeeper displays the bangles in the form of a square then he is left with 38 bangles. If he wanted to increase the size of square by one unit each side of the square he found that 25 bangles fall short of in completing the square. The actual number of bangles which he had with him in the shop was ________.
In the equation 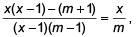 the roots are equal when m = ________.
the roots are equal when m = ________.
In the Maths Olympiad of 2020 at Animal Planet, two representatives from the donkey’s side, while solving a quadratic equation, committed the following mistakes.
(i) One of them made a mistake in the constant term and got the roots as 5 and 9.
(ii) Another one committed an error in the coefficient of x and he got the roots as 12 and 4.
But in the meantime, they realised that they are wrong and they managed to get it right jointly. Find the quadratic equation.
A man walks a distance of 48 km in a given time. If he walks 2 km/hr faster, he will perform the journey 4 hrs before. His normal rate of walking, is ________.
Swati can row her boat at a speed of 5 km/hr in still water. If it takes her 1 hour more to row the boat 5.25 km upstream than to return downstream, find the speed of the stream.
₹ 6500 were divided equally among a certain number of persons. If there had been 15 more persons, each would have got ₹ 30 less. Find the original number of persons.