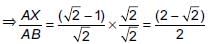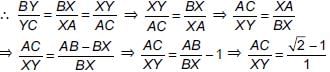Math Olympiad Test: Triangles - 4 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Triangles - 4
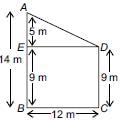
Two poles of height 9 m and 14 m stand on a plane ground. If the distance between their feet is 12 m, then the distance between their tops is
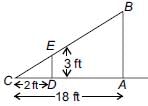
If a tree casts a 18 feet shadow and at the same time, a child of height 3 feet casts a 2 feet shadow, then the height of the tree is
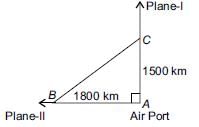
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1(1/2) hours?
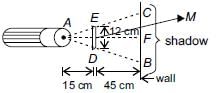
A 12 cm rod is held between a flashlight and a wall as shown. Find the length of the shadow on the wall if the rod is 45 cm from the wall and 15 cm from the light.
In the given figure, ABC is a right triangle right-angled at B. AD and CE are the two medians drawn from A and C respectively. If AC = 5 cm and AD = 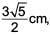 then the length of CE is
then the length of CE is
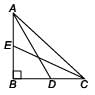
Mason Construction wants to connect two parks on opposite sides of town with a road. Surveyors have laid out a map as shown. The road can be built through the town or around town through point R. The roads intersect at a right angle at point R. The line joining Park A to Park B is parallel to the line joining C and D.
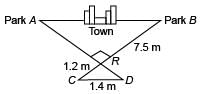
(i) What is the distance between the parks through town?
(ii) What is the distance from Park A to Park B through point R?
In the given figure,the line segment XY is parallel to side AC of ΔABC and it divides the triangle into two parts of equal area. Then, find
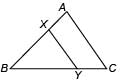
(i) AX : AB (ii) AC/XY
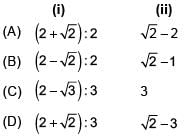
P and Q are the mid-points of the sides CA and CB respectively of a DABC, right angled at C, then find:
(i) 4AC2 + BC2
(ii) 4BC2 + AC2
(iii) 4(AQ2 + BP2)




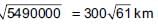

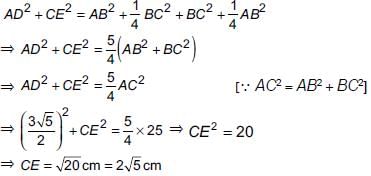
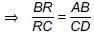 ... (i)
... (i)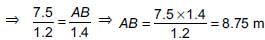
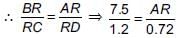
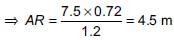

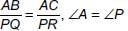
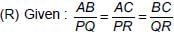
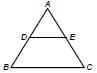
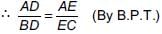
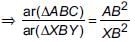 ...(i)
...(i)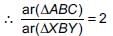 ...(ii)
...(ii)