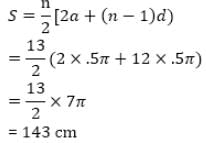Mathematics Mock Test - 1 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Mathematics Mock Test - 1
Cost of 40 books is equal to the market price of 16 Book. If seller make 100% profit then find the discount percentage given by him to buyer.
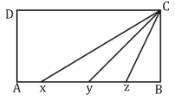
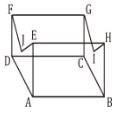
Side AB of a rectangle ABCD is divided into four equal parts as shown in the figure; find the ratio of the area of Δxyc and area of  ?
?
 ?
?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In this given figure an equilateral triangle based prism is cut off a cube of side of 3 cm as shown in figure. Find the total surface area (in cm2) of remaining structure.

The average weight of 3 men A,B and C is 85 kg another man D joins the group and the average now become 81 kg. If another man E whose weight is 4 kg more than that of D, replaces A then the average weight of B, C, D and E becomes 80 kg. What is the weight of A?
If sin θ + cos θ = a and sec θ +cosec θ = b, then value of b(a2 -1) is equal to:
If a2 + b2 + c2 = 2( 3a - 4b - 6c) - 61. Find value of (a-b-c).
Work done by (x + 4) men in (x + 5) days is equal to the work done by (x – 5) men in (x + 20) days. The value of x is
What is the number of distinct triangles with integral valued sides and perimeter as 14?
The train A left Delhi at noon sharp. Four hours later, another train B started from Delhi in the same direction. The train B overtook the train A at 10 p.m. Find the average speed of the both trains over this journey if the sum of their speed is 80 km/h.
If a secθ + b tanθ =1 and a2 sec2θ - b2 tan2 = 5, then a2b2 + 4a2 is equal to
If x varies inversely as (y2 - 1) and is equal to 24 when y = 10, then the value of x when y = 5 is
Which term of the AP: 121, 117, 113……… is its first negative term.
If cot θ + cos θ = p and cot θ - cos θ = q, then (p2 - q2)2 in terms of p and q is-
A dishonest dealer defrauds to the extent of 10% in buying and 20% in selling and claims that he earns only 10% profit what will be the gain percent on his outlay.
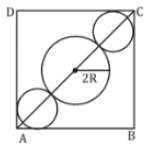
In given figure ABCD is a square in which three circles are drawn touching one another. Radius of two smaller circles is R units and bigger circle is 2R units. Diagonal AC of the square passes through the center of all the circles. What is the ratio of the radius of the smaller circles to the side of the square?
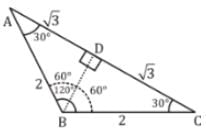
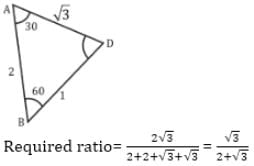
The angles of a triangle are in the ratio of 4 : 1 : 1. Then the ratio of the longest side to the perimeter is
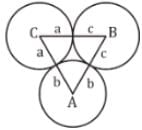
Three circles of radius a, b, c touch each other externally. The area of the triangle formed by joining their centre is
A man makes 80 articles in the 1st hour. His efficiency decreases by 25% in the 2nd hour, increases by 40% in the 3rd hour, decreases by 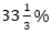 in the 4th hour and increases by
in the 4th hour and increases by 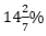 in the 5th hour (his efficiency increases or decreases with respect to the efficiency in previous hour). If he works for 5 hours, then find the average of total article made by the man in 5 hours.
in the 5th hour (his efficiency increases or decreases with respect to the efficiency in previous hour). If he works for 5 hours, then find the average of total article made by the man in 5 hours.
Let A, B, C, D be the angles of a quadrilateral. If they are concyclic then the value of cos A + cos B + cos C + cos D is
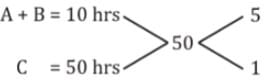
A can do as much work as B and C together can do. A and B can together do a piece of work in 10 hours and C can do it in 50 hrs. Then, time that B needs to do the work alone is –
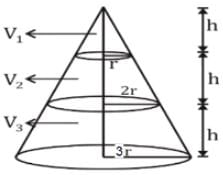
If a right circular cone is cut into three solids of volumes V1,V2, and V3 by two cuts which are parallel to the base and trisects the altitude then V1,V2, and V3 is
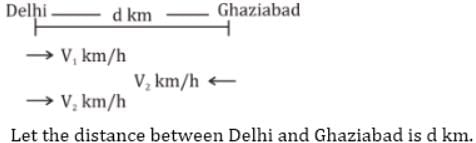
A man goes from Delhi to Ghaziabad at v1 km/h, goes back from Ghaziabad to Delhi at v2 km/h and again Delhi to Ghaziabad at v2 km/h. The average speed of man is
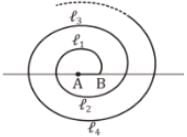
A spiral is made up of successive semicircles with centers alternately at A and B, starting with center at A of radii 0.5 cm, 1.0 cm, 1.5 cm…………as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles?
|
23 docs|73 tests
|
|
23 docs|73 tests
|






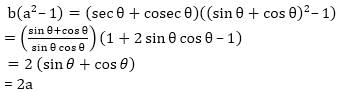
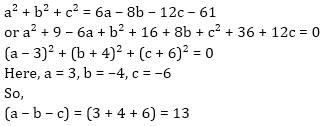
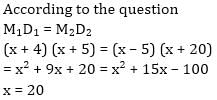
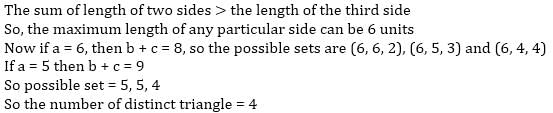
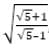 , then the value of 5x2 - 5x - 1 is
, then the value of 5x2 - 5x - 1 is 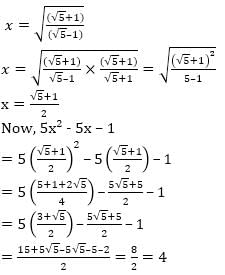

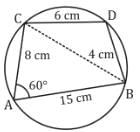
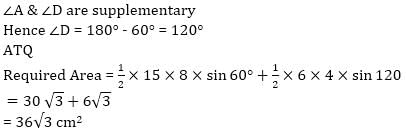

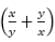 and
and 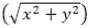 is
is 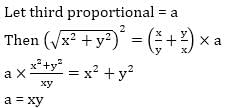
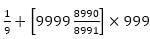 is equal to
is equal to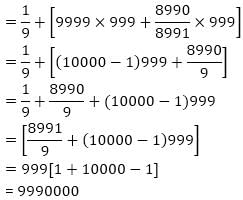
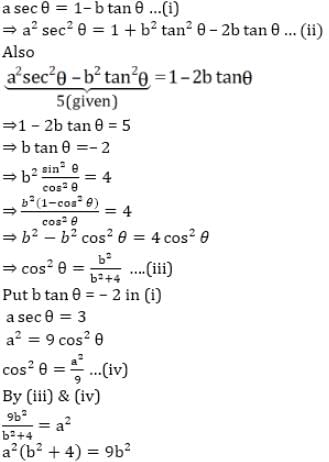

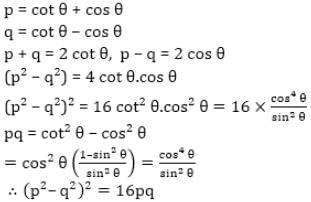

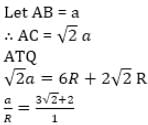

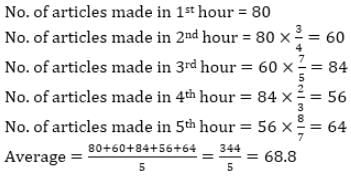
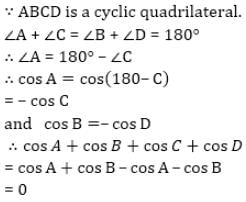
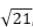 , then the value of
, then the value of 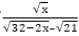 is
is 

 , then the value of
, then the value of 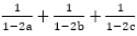 is:
is: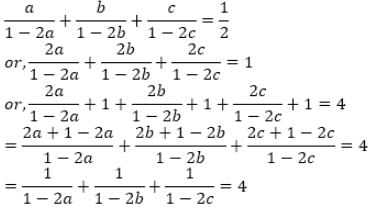
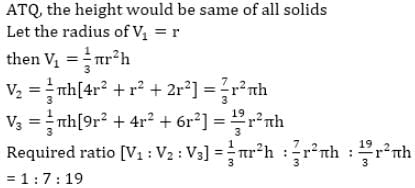

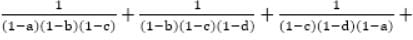
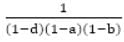 is
is