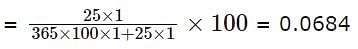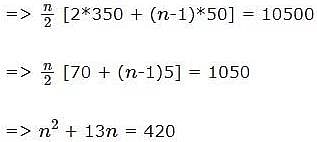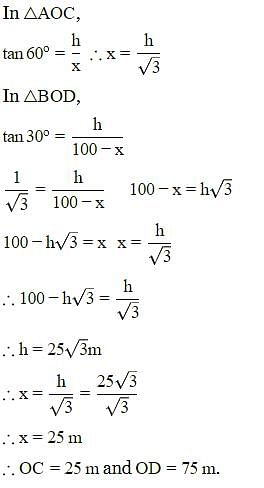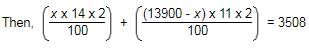Mathematics Mock Test - 10 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Mathematics Mock Test - 10
The sum of the first 100 natural numbers, 1 to 100 is divisible by:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the remainder when 73 * 75 * 78 * 57 * 197 * 37 is divided by 34.
If equal numbers of people are born on each day, find the approximate percentage of the people whose birthday will fall on 29th February. If we are to consider people born in 20th century (1901-2000) and assuming no deaths.
Seema has joined a new Company after the completion of her B.Tech from a reputed engineering college in Chennai. She saves 10% of her income in each of the first three months of her service and for every subsequent month, her savings are Rs. 50 more than the savings of the immediate previous month. If her joining income was Rs. 3000, her total savings from the start of the service will be Rs. 11400 in:
Dev and Om are among 22 students who write an examination. Dev scores 82.5. The average score of the 21 students other than Om is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Dev. The score of Om is.
The average age of a family of 5 members is 20 years. If the age of the youngest member is 10 years, what was the average age of the family at the birth of the youngest member?
The sum of three numbers x, y, z is 5000. If we reduce the first number by 50, the second number by 100, and the third number by 150, then the new ratio of x & y = 4 : 5 & the new ratio of y & z =3 : 4. What is the value of x + y ?
Two sprinters run the same race of100 m One runs at a speed of 10 m/s and the other runs at 8 m/s. By what time will the first sprinter beat the other sprinter?
Two rabbits start simultaneously from two rabbit holes towards each other. The first rabbit covers 8% of the distance between the two rabbit holes in 3 hours, The second rabbit covered 7 / 120 of the distance in 2 hours 30 minutes. Find the speed (feet / h) of the second rabbit if the first rabbit travelled 800 feet to the meeting points.
The sum and the product of the roots of the quadratic equation x2 + 20x + 3 = 0 are?
For all x, x2 + 2ax + (10 − 3a) > 0, then the interval in which a lies, is?
Consider the equation:
|x-5|2 + 5 |x - 5| - 24 = 0
The sum of all the real roots of the above equationis:
a, b, c are integers, |a| ≠ |b| ≠|c| and -10 ≤ a, b, c ≤ 10. What will be the maximum possible value of [abc – (a + b + c)]?
If cos A + cos2 A = 1 and a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0. Find the value of a+b / c+d
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. Find a point between them on road, angles of elevation of their tops are 30∘ and 60∘. The height of each pole in meter, is:
The least multiple of 7, which leaves a remainder of 4, when divided by 6, 9, 15 and 18 is:
The greatest number of four digits which is divisible by 15, 25, 40 and 75 is:
125 toffees cost Rs. 75. Find the cost of one million toffees if there is a discount of 40% on the selling price for this quantity.
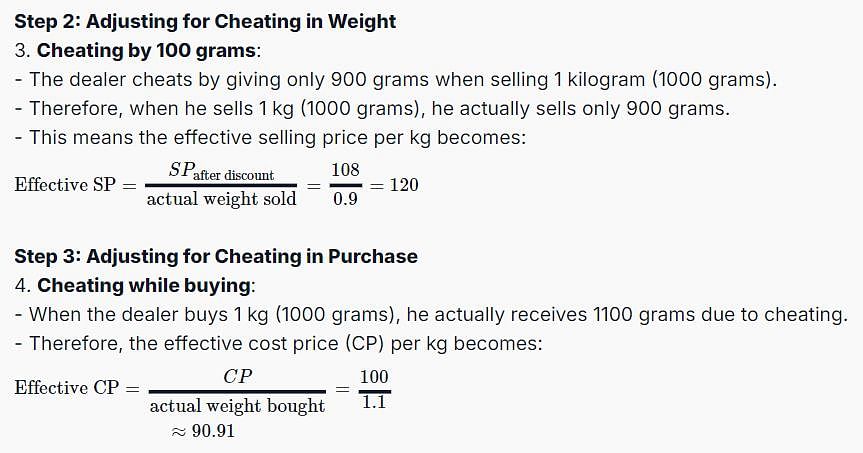
A dishonest dealer marks up the price of his goods by 20% and gives a discount of 10% to the customer. Besides, he also cheats both his supplier and his buyer by 100 grams while buying or selling 1 kilogram. Find the percentage profit earned by the shopkeeper.
Mr. Thomas invested an amount of Rs. 13,900 divided in two different schemes A and B at the simple interest rate of 14% p.a. and 11% p.a. respectively. If the total amount of simple interest earned in 2 years be Rs. 3508, what was the amount invested in Scheme B?
A man took loan from a bank at the rate of 8% p.a. simple interest. After 4 years he had to pay Rs. 6200 interest only for the period. The principal amount borrowed by him was:
A dice is thrown. What is the probability that the number shown in the dice is divisible by 3?
There are 15 boys and 10 girls in a class. If three students are selected at random, what is the probability that 1 girl and 2 boys are selected?
A train having a length of 1/4 mile , is traveling at a speed of 75 mph. It enters a tunnel 3 ½ miles long. How long does it take the train to pass through the tunnel from the moment the front enters to the moment the rear emerges?
I. a2 - 7a + 12 = 0,
II. b2 - 3b + 2 = 0 to solve both the equations to find the values of a and b?
I. x2 + 5x + 6 = 0,
II. y2 + 9y +14 = 0 to solve both the equations to find the values of x and y?
|
23 docs|73 tests
|
|
23 docs|73 tests
|