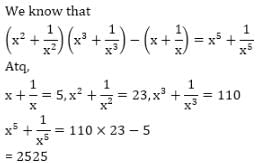Mathematics Mock Test - 2 - CDS MCQ
30 Questions MCQ Test - Mathematics Mock Test - 2
If 2 boys consume 2x calories every y/2 days. 8 girls consume z/2 calories every y days. How many calories will 12 girls & 12 boys consume in 12 days ?
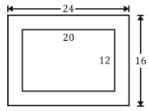
Adjacent sides of the rectangular plot are 20meter and 12meter respectively. A dishonest builder in an attempt to make more profit has encroached 2meter of land on all four sides and then by doing the fencing of the entire plot, he sold it to a customer at Rs 55 sq meter. How much extra money has been made by the builder?
In an Election 10% of the voters on the voters’ list did not cast their votes and 60 voters cast their ballot papers blank. there were only two candidates. The winner was supported by 47% of all the votes in the list and he got 308 votes more than his rival the Number of voters on the list was.
The ratio of numbers of boys to the number of girls in a school of 432 pupils is 5 : 4. When some new boys & girls are admitted, the no. of boys increases by 12 and the ratio of the boys to girls changes to 7 : 6. Then number of new girls admitted is:
If X2. is a perfect cube, then which of the following statement is always true.
B was born when A was 4 yrs 7 months old and C was born When B was 3 yrs 4 months old. When C was 5 yrs 2 months old, then their average age was
Abhaya sell his office at a loss of 10%, if he had sold it for Rs. 245 more he would have gained 25% profit. What will be his gain or loss present if he sold it Rs. 595?
Neha’s weight is 140% of tina’s weight Mina’s weight is 90% of Lina’s weight. Lina’s weight is twice as much as that of Tina. If Neha’s weight is x% of Mina’s weight then x is equal to-
Two barges, traveling at 5 & 10 kms per hour, head directly towards each other. They begin at a distance of 20 kms from each other. How far apart are they (in kms) one min before they collide?
Arun borrowed a sum of Rs. 4000 at 5% pa SI for Ramu. He returned the amount with interest after 2 yrs. Ramu returns to Arun 3% of the total amount returned. How much did Ramu received overall?
Let α & β be the roots of eqn. x2 - 6x - 2 = 0. If αn = αn + βn , for n ≥ 1, then value of 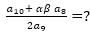
If a, b, c are distinct +ve real numbers and a2 + b2 + c2 = 1 then ab + bc + ca =?
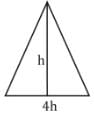
The base of a triangular field is four times its height. If the cost of cultivating the field at Rs. 15.5 per hectare is Rs. 1116, find the base length (in meter) of the triangular field? (1 hectare = 10000 m2 )
Find the perimeter (in cm) of a regular quadrilateral with a diagonal of length 3√2 cm?
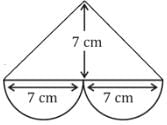
Find the cost of Flooring of the heart shaped pool mentioned in the figure if the rate of flooring is Rs 150 per sq meter and depth of the pool is 2 meters?
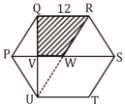
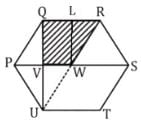
Find the area of the shaded region where PQRSTU is a regular hexagon of side 12 cm, & W is its centroid.
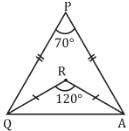
Find ∠PQR of the given isosceles ΔAPQ, when PQ = PA & QR = RA?
If (tan θ + cot θ) = 1, sin θ + cos θ = b with 0° < θ < 90° then relation between a and b is —
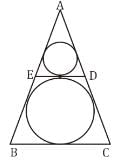
Given an equilateral ∆ABC inscribing two circles as shown in the figure below. If DE tangent to both the circles. Then find the ratio of perimeters of the two circles.
A Toy consists of a base that is the section of a sphere and a conical top. The volume of the conical top is 30 π sq. units and its height is 10 units. The total height of the toy is 19 unit. Then the volume of the sphere (in cubic units) is.
Amit plans to buy a scooter for his sister for which he saves Rs. 15625 at the start of every year for 3 year. If the rate of CI is 4% pa. then amount at which he plans to buy the scooter is (in Rs.)
What is the value of a, if (x -a) is a factor of (x3 - a2x + x + 1)?


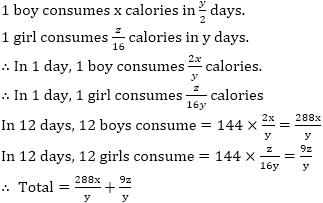


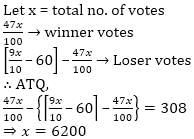

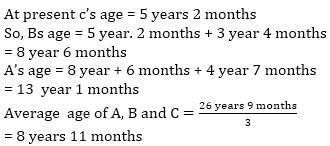
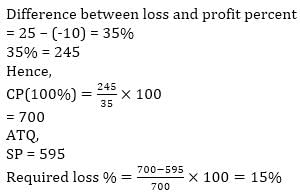



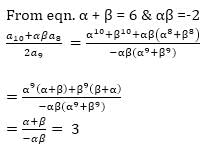
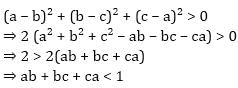
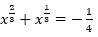
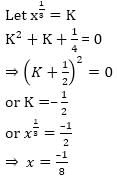
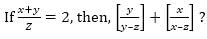
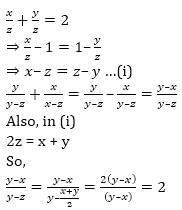

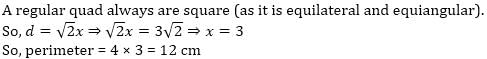


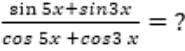
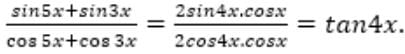
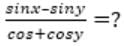
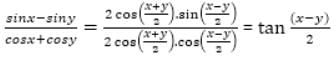

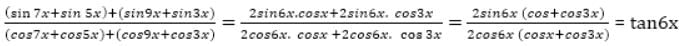
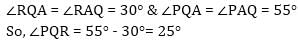
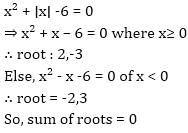
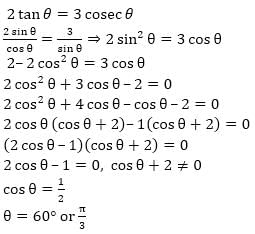
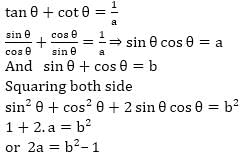
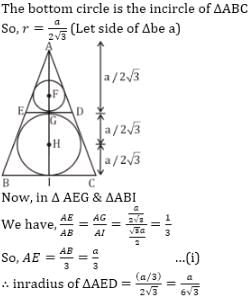
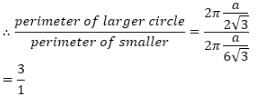
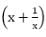 = 5 then the value of
= 5 then the value of 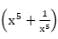 is
is