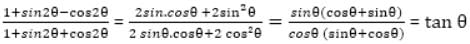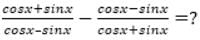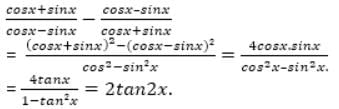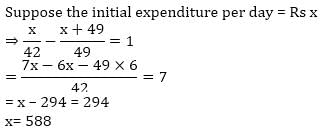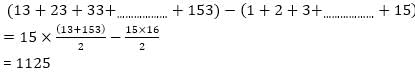Mathematics Mock Test - 5 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Mathematics Mock Test - 5
If 5 men or 8 women or 12 boys can do a work in 24 days working 8 hrs a days, how many men must be associated with 16 women and 12 boys to do another with 6 times as great in 30 days working 6 hours per day ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
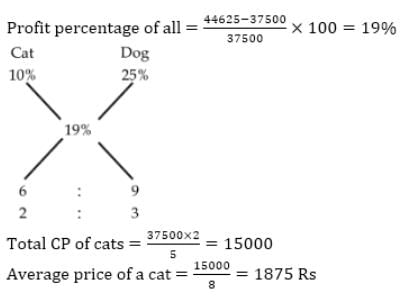
8 Cats and 6 dogs cost me Rs. 37500. I sell them for Rs. 44625 making a profit of 10 percent on cat and 25 percent on dogs what is the average cost of each cat?
Gold is 14 times as heavy as water and copper is 6 times as heavy as water. In what ratio should to these be mixed to get an alloy 11 times as heavy as water.
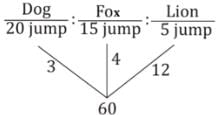
A dog takes 7 jumps when a fox takes 10 jumps & a lion takes 12 jumps when a fox takes 10 jumps. And distance of 20 jumps of dog, 15 jumps of fox & 5 jumps of lion are equal. Find the ratio of their speeds.
When P liter oil is poured into a vessel, the vessel remains K% empty. How Many litres do we need to pour in the vessel so that the vessel is full.
In a town 60% of the adult population is male, a% of the adult Males and b% adult females are Educated. The total Number of Educated adult Males and uneducated adult females is equal in number to the total Number of Uneducated adult Males and Educated adult females if a and b are both integers. Which of the following could be the set of values (a, b)?
A man takes 8 hrs to walk to a certain place and ride back. However, he could have Saved 2 hrs, if he had covered both ways by riding. How long would he take to walk both ways?
If the difference between CI and SI on a sum of money for 3 years is Rs. 5103, then what is the sum if the rate of interest in both cases is 15% (in Rs.)
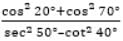 - 2 cot 58° tan 32°- 4 tan 13° tan 37° tan 53° tan 77° tan 45° + 2 cosec2 58° =?
- 2 cot 58° tan 32°- 4 tan 13° tan 37° tan 53° tan 77° tan 45° + 2 cosec2 58° =?
If a man and a boy can build one and a half walls in 1.5 days, then how many walls do 7 men build in 9 days if efficiency of a man and a boy are in ratio 2:1?
Rs. 6000 becomes Rs. 7,200 in 2 years at a certain rate of SI, If the rate becomes 1.5 times of itself, the amount (in Rs.) of the same principal in 15 yrs will be.
CI of 7th year & 5th years respectively are 961 & 576 Rs. Find the rate of interest ? (in %)
If x + y + z = 22 & xy + yz + zx = 35, then what is the value of (x - y)2 + (y - z)2 + (z-x)2?
There were 42 students in a hostel. If the number of students is increased by 7 the expenditure on food increases by 49 per day while the average expenditure is reduced by Re 1. What was the initial expenditure on food per day?
The highest score of a batsman in an innings was 2/9 of the total score and the next highest score of another batsman was 2/9 of the remaining total score. These scores differ by 8 runs. What was the total score in the innings?
|
23 docs|73 tests
|
|
23 docs|73 tests
|



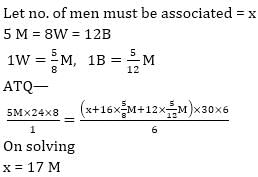

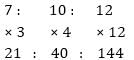
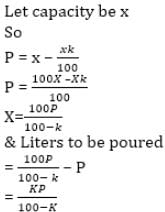
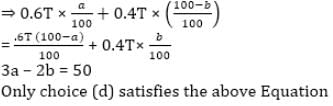
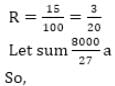



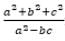 is
is 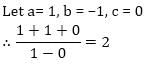
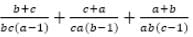 =?
=?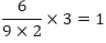
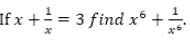
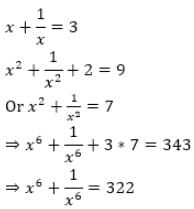
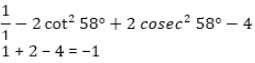
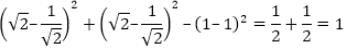
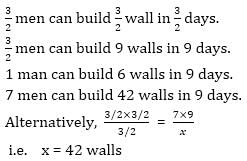
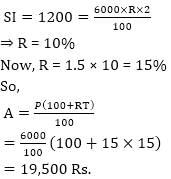
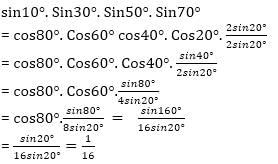
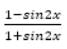
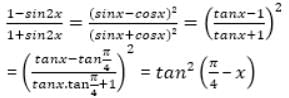

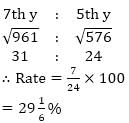
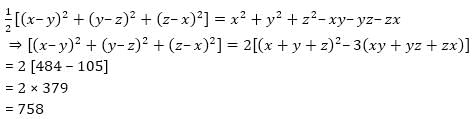
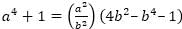 , then, a4 + b4 =?
, then, a4 + b4 =? 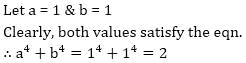
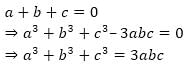
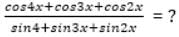
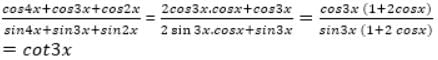
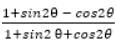 =?
=?