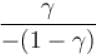Maxwell's Relations MCQ Level – 2 - IIT JAM MCQ
10 Questions MCQ Test - Maxwell's Relations MCQ Level – 2
Ratio of the adiabatic coefficient of expansion which is 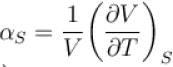 to the isobaric coefficient of expansion
to the isobaric coefficient of expansion 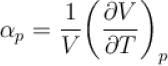 is
is
Select one:
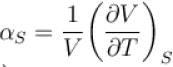 to the isobaric coefficient of expansion
to the isobaric coefficient of expansion 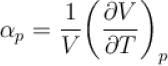 is
isSelect one:
For a perfect gas Joule - Thomson cofficient µ is equal to
Select one:
Select one:
Calculate under what pressure (atm) water would boil at 150°C. If the change in specific volume when 1 gram of water is converted into steam is 1676cc. Given, latent heat of vaporization of steam = 540 cal/g; J = 4.2×107 erg/cal and one atmosphere pressure = 106 dynes/cm2
Select one:
Select one:
The normal boiling point of benzene is 80°C. The latent heat of vaporization is 380 Joule/g, density of vapour at boiling points is 4g/litre and that of the liquid 0.9g/cm3 then the boiling point of benzene under a pressure of 80 cm of mercury.
Select one:
For any substance, the ratio of adiabatic and isothermal elasticities which are  and
and 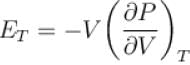 respectively is equal to :
respectively is equal to :
Select one:
If C1 and C2 represents the specific heat of a liquid and its saturated vapour respectively and L is the latent heat of the vapour then clausius latent heat equation is given by :
Select one:
The Gibb’s function G in thermodynamics is defined as
G = H – TS
(where, H = Enthalpy, T = Temperature, S = Entropy)
In an isothermal, isobaric, reversible process, G
Select one:
The thermodynamical relation expressing TdS equation
Select one:
The ratio of the adiabatic to the isochoric pressure coefficient of expansion is
Select one:


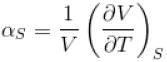

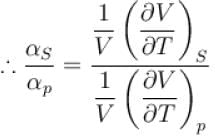
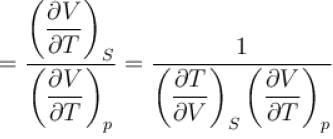
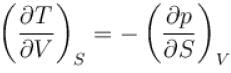

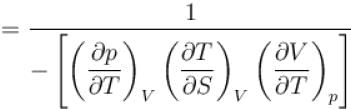
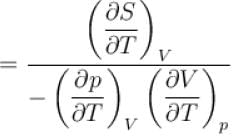
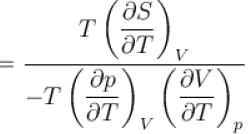
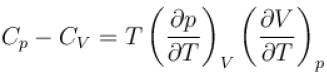
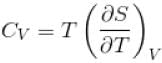
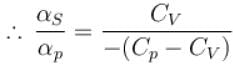
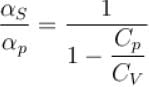
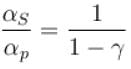
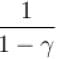
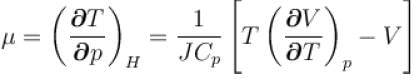
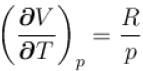
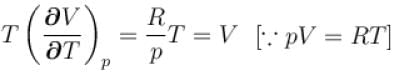
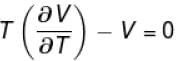

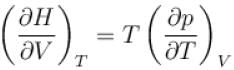
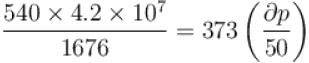

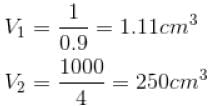
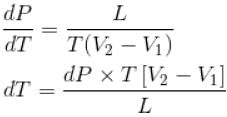
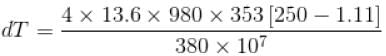
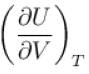 is equal to
is equal to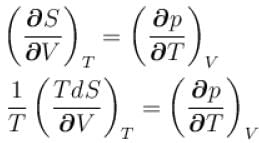
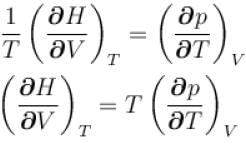
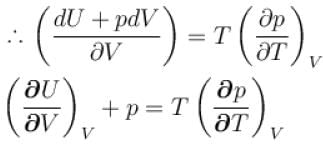
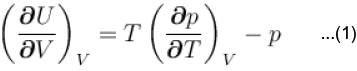
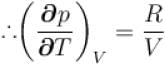
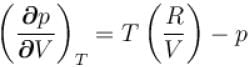
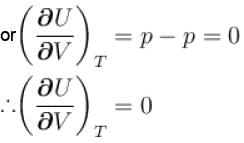
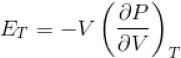
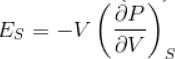
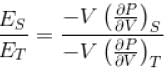
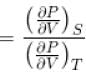

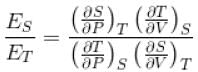
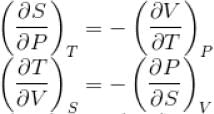
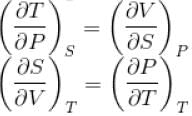

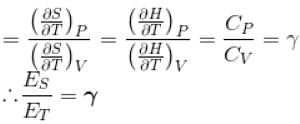
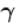
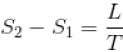 ...(i)
...(i)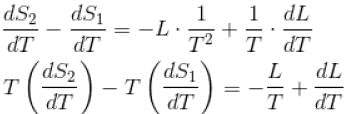
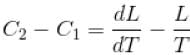
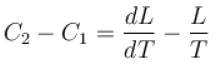

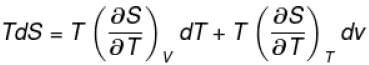
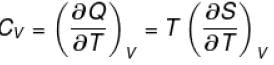
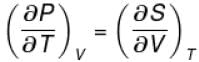
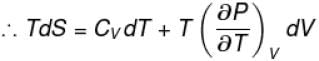
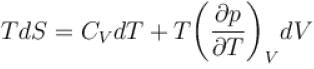
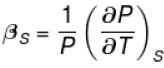
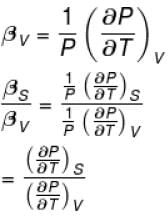
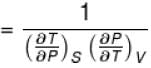
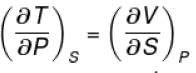
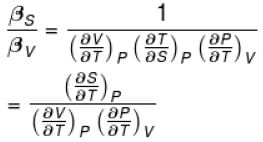
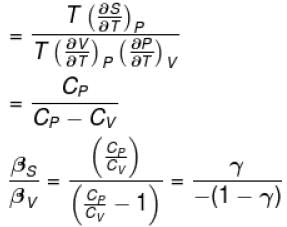 The correct answer is:
The correct answer is: