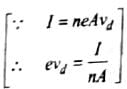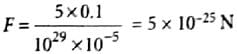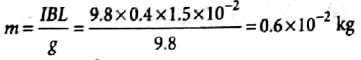NCERT Based Test: Magnetic Force - NEET MCQ
15 Questions MCQ Test NCERTs at Fingertips: Textbooks, Tests & Solutions - NCERT Based Test: Magnetic Force
When a magnetic compass needle is carried nearby to a straight wire carrying current, then
(i) the straight wire cause a noticeable deflection in the compass needle.
(ii) the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire
(i) the straight wire cause a noticeable deflection in the compass needle.
(ii) the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire
Which one of the following is not correct about Lorentz force?
A strong magnetic field is applied on a stationary electron. Then the electron
In an inertial frame of reference, the magnetic force on a moving charged partic le is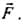 Its value in another inertial frame of reference will be
Its value in another inertial frame of reference will be
The magnetic force  on a current carrying conductor of length l in an external magnetic field
on a current carrying conductor of length l in an external magnetic field 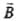 is given by
is given by
A straight wire having mass of 1.2 kg and length of 1m carries a current of 5A. If the wire is suspended in mid-air by a uniform horizontal magnetic field, then the magnitude of field is
A circular loop of radius R carrying a current I is placed in a uniform magnetic field B perpendicular to the loop. The force on the loop is
A 2.5 m long straight wire having mass of 500 is suspended in mid air by a uniform horizontal magnetic field B. If a current of 4 A is passing through the wire then the magnitude of the field is (Take g = 10 m s-2)
A current of 10 A is flowing in a wire of length 1.5 m. A force of 15 N acts on it when it is placed in a uniform magnetic field of 2 T. The angle between the magnetic field and the direction of the current is
The horizontal component of earth's magnetic field at a certain place is 3.0 x 10-5 T and having a direction from the geographic south to geographic north. The force per unit length on a very long straight conductor carrying a steady current of 1.2 A in east to west direction is
A circular coil of 20 turns and 10 cm radius is placed in a uniform magnetic field of 1.10T normal to the plane of the coil. If the current in the coil is 5A, cross-sectional area is 10-5 m2 and coil is made up of copper wire having free electron density about 1029 m-3, then the average force on each electron in the coil due to magnetic field is
The magnetic force per unit length on a wire carrying a current of 10 A and making an angle of 45° with the direction of a uniform magnetic field of 0.20 T is
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then megnetic force on the wire is
A rectangular coil ABCD is hung from one side of a balance as shown in figure. A 500 g mass is added to the other arm to balance the weight of the coil. A current of 9.8 A is passed through the coil and a constant magnetic field of 0.4 T acting inward (in xz plane) is switched on such that only arm CD of length 1.5 cm lies in the field. The additional mass m must be added to regain the balance is
Which one of the following is correct statement about magnetic forces?
|
237 docs|243 tests
|


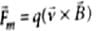
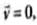 for stationary charge ∴
for stationary charge ∴ 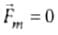 .
.
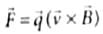
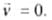
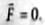 So, electron will remain stationary.
So, electron will remain stationary.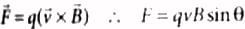
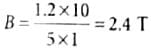
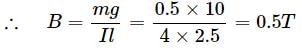
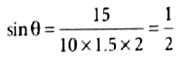 or θ = 30°
or θ = 30°