NCERT Based Test: Motion in a Magnetic Field - Free MCQ with solutions
MCQ Practice Test & Solutions: NCERT Based Test: Motion in a Magnetic Field (5 Questions)
You can prepare effectively for NEET Physics Class 12 with this dedicated MCQ Practice Test (available with solutions) on the important topic of "NCERT Based Test: Motion in a Magnetic Field". These 5 questions have been designed by the experts with the latest curriculum of NEET 2026, to help you master the concept.
Test Highlights:
- - Format: Multiple Choice Questions (MCQ)
- - Duration: 5 minutes
- - Number of Questions: 5
Sign up on EduRev for free to attempt this test and track your preparation progress.
A charged particle is moving on circular path with velocity v in a uniform magnetic field B, if the velocity of the charged particle is doubled and strength of Magnetic field is halved, then radius becomes
Detailed Solution: Question 1
An electron of energy 1800 eV describes a circular path in magnetic field of flux density 0.4 T. The radius of path is (q = 1.6 x 10-19 C, me = 9.1 x 10-31 kg)
Detailed Solution: Question 2
Two α-partides have the ratio of their velocities as 3 : 2 on entering the field. If they move in different circular paths, then the ratio of the radii of their paths is
Detailed Solution: Question 3
When a positively charged particle enters a uniform magnetic field with uniform velocity, its trajectory can be (i) a straight line (ii) a circle (iii) a helix.
Two particles of equal charges after being accelerated through the same potential difference enter in a uniform transverse magnetic field and describe circular paths of radii R1 and R2. Then the ratio of their respective masses (M1/M2) is
Detailed Solution: Question 5
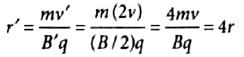
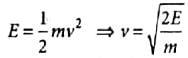
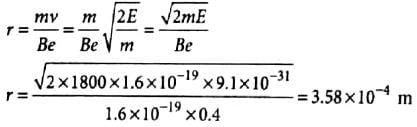
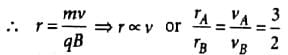
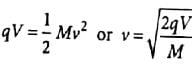
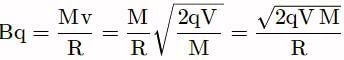Using (i)
74 videos|347 docs|82 tests |
