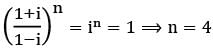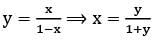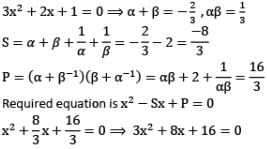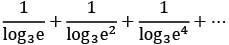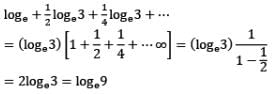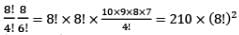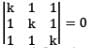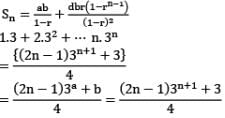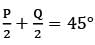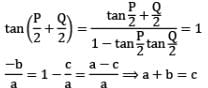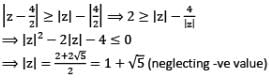NDA II - Mathematics Question Paper 2017 - NDA MCQ
30 Questions MCQ Test - NDA II - Mathematics Question Paper 2017
If x + log10(1 + 2x ) = xlog10 + log10 6 then x
is equal to
is equal to
The remainder and the quotient of the binary division
(101110)2 ÷ (110)2 are respectively
(101110)2 ÷ (110)2 are respectively
The matrix A has x rows and x + 5 columns. The matrix B has y rows and 11 − y columns. Both AB and BA exist. What are the values x and x respectively?
If Sn = nP 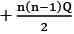 , where Sn denotes the sum of the first n terms of an AP, then the common difference is
, where Sn denotes the sum of the first n terms of an AP, then the common difference is
The roots of the equation (q − r)x2 + (r − p)x + (p − q) = 0 are
If E is the universal set and A = B ∪ C, then the set
E − (E − (E − (E − (E − A)))) is same as the set
If A={x:x is a multiple of 2},B={x:x is a multiple of 5} and C={x:x is a multiple of 10}, then A∩(B∩C) is equal to
If α and β are the roots of the equation 1 + x + x2 = 0 , then the matrix product 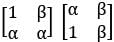 is equal to?
is equal to?
If |a| denotes the absolute value of an integer, then which of the following are correct?
I.|ab| = |a||b|
II. |a + b| ≤ |a| + |b|
III. |a − b| ≥ |a| − |b|
Q. Select the correct answer using the code given below.
How many different permutations can be made out of the letters of the word “PERMUTATION”?
If A = 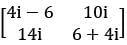 and k =1/2i, where i =
and k =1/2i, where i =
√−1 , then kA is equal to
The sum of all real roots of the equation
|x − 3|2 + |x − 3| − 2 = 0 is
If is given that the roots of the equation x2 − 4x − log3 P = 0 are real. For this, the minimum value of P is
If A is a square matrix, then the value of adj AT − (adj A)T is equal to
The value of the product
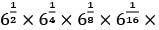 … up to infinite terms is
… up to infinite terms is
The value of the determinant
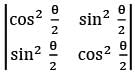 forall values of θ, is
forall values of θ, is
The number of terms in the expansion of (x + a)100 + (x − a)100 after simplification is
In the expansion of (1 +)50 , the sum of the coefficients of odd powers of x is
If a, b, c are non-zero real numbers, then the inverse of the matrix
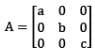
A person is to count 4500 notes. Let an denote the number of notes he counts in the nth minute.
If a1 = a2 = a3 = . . = a10 = 150 , and
a10 , a11 , a12 . .. are in AP with the common difference −2 , then the time taken by him to count all the notes is
The smallest positive integer n for which
 n = 1 , is
n = 1 , is
If we define a relation R on the set N × N as (a, b) R (c, d) ⟺ a + d = b + c for all (a, b), (c, d) ∈ N × N, then the
If y = x + x2 + x3 + ⋯ up to infinite terms, where x < 1 , then which of the following is correct?
If α and β are the roots of the equation 3x2 + 2x + 1 = 0 , then equation whose roots are α + β−1 and β + α−1 is
A tea party is arranged for 16 people along two sides of a long table with eight chairs on each side. Four particular men wish to sit on one particular side and two particular men on the other side. The number of ways they can be seated is
The system of equation kx + y + z = 1,
x + ky + z = k and x = y + kz = k2 has nosolution if k equals
If 1.3 + 2.32 + 3.33 + ⋯ + n. 3n 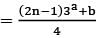
Then a and b are respectively
In △ PQR, ∠R 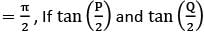 are the roots of the equation ax2 + bx + c = 0, then which one of the following is correct?
are the roots of the equation ax2 + bx + c = 0, then which one of the following is correct?
If 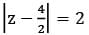 , then the maximum value of |z| is equal to
, then the maximum value of |z| is equal to




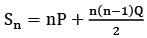
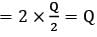
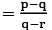
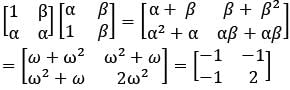
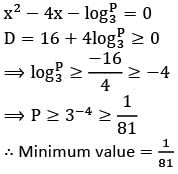
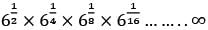
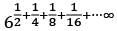
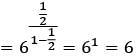
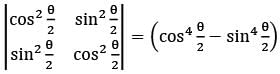

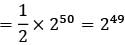
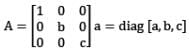
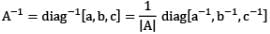
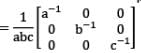
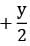 [2 × 150 + (y − 1)(−2)] = 4500
[2 × 150 + (y − 1)(−2)] = 4500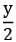 (302 − 2y) = 3150 ⟹ y2 − 151y + 3150 = 0
(302 − 2y) = 3150 ⟹ y2 − 151y + 3150 = 0