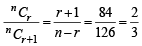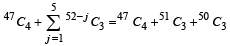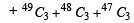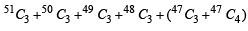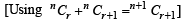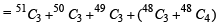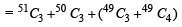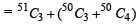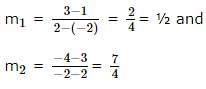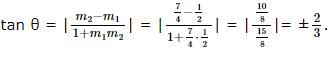NDA Mock Test: Mathematics - 4 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2025 - NDA Mock Test: Mathematics - 4
Let R = {(P, Q) : OP = OQ , O being the origin} be an equivalence relation on A. The equivalence class [(1, 2)] is
Directions: Consider the following statements regarding two different non-zero integers p and q.
1. For (p + q) to be less than (p – q), q must be negative.
2. For (p + q) to be greater than (p – q), both p and q must be positive.
Which of the above statements is/are correct?
Let a relation T on the set R of real numbers be T = {(a, b) : 1 + ab < 0, a, ∈ R}. Then from among the ordered pairs (1, 1), (1, 2), (1, -2), (2, 2), the only pair that belongs to T is________.
For real number x and y, we write xRy ⇔ x-y + √2 is an irrational number. Then the relation R is:
If A = [aij]2×2 where aij= i + j, then A is equal to
The matrix of the transformation ‘reflection in the line x + y = 0 ‘ is
The system of equations kx + 2y – z = 1,
(k – 1)y – 2z = 2
(k + 2)z = 3 has a unique solution, if k is
The solution of the quadratic equation: 2x2 + 3ix + 2 = 0
nCr–1 = 36, nCr = 84 and nCr + 1 = 126, then r is : (1979)
Ten different letters of an alphabet are given. Words with five letters are formed from these given letters. Then the number of words which have at least one letter repeated are (1982 - 2 Marks)
The value of the expression 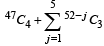 is equal to (1982 - 2 Marks)
is equal to (1982 - 2 Marks)
The largest coefficient in the expansion of (1+x)24 is:
In the expansion of (1+a)m+n which of the following is true?
The sum of all 2-digited numbers which leave remainder 1 when divided by 3 is
If A (-2, 1), B (2, 3) and C (-2, -4) are three points, find the angle between the straight lines AB and BC.
If the slope of the line passing through the points (2, 5) and (x, 1) is 2, then x = ______.
Equation of line parallel to the line Ax + By + C = 0 is:
The equation of the line parallel to the line 2x – 3y = 1 and passing through the middle point of the line segment joining the points (1, 3) and (1, –7), is:
The equation of a line whose perpendicular distance from the origin is 3 units and the angle made by perpendicular with the positive x-axis is 30° is:
The distance between the pair of points (7,8) and (4,2) ,if origin is shifted to (1,-2) ,would be
What will be the value of ‘p” if the equation of the straight line 3x + 5y = 10 gets changed to 3x + 5y = p after shifting the origin at (2,2) ?
In drilling world’s deepest hole, it was found that the temperature T in degree Celsius, x km below the surface of Earth, was given by T = 30 + 25 (x – 3), 3 < x < 15. If the required temperature lies between 200o C and 300o C, then the depth, x will lie between
A solution of 10% boric acid is to be diluted by adding a 4% boric acid solution to it. The resulting mixture is to be more than 5% but less than 8% boric acid. If we have 750 litres of the 10% solution, then the quantity of the 4% solution that has to be added will lie between
The length of the chord joining the point (4 cos θ, 4 sin θ) and 4 (cos(θ+60o), 4 sin(θ + 60o)) of the circle x2+y2 = 16 is
|
2 docs|101 tests
|



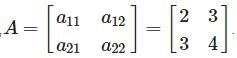
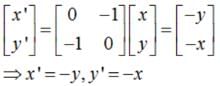
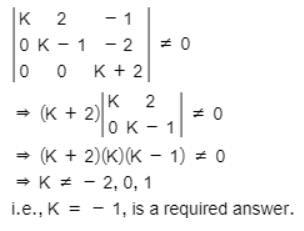
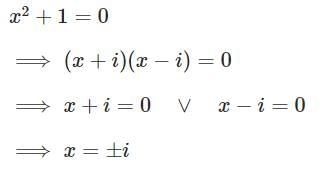
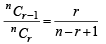
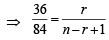
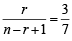
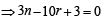 ....(1)
....(1)