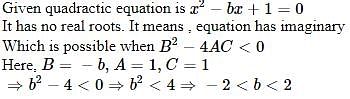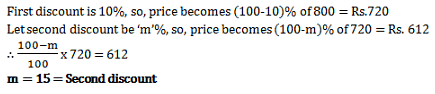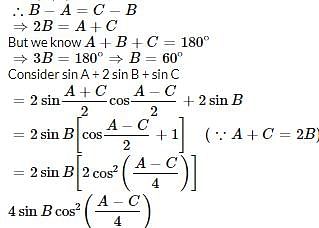NDA Mock Test: Mathematics - 9 - NDA MCQ
30 Questions MCQ Test NDA (National Defence Academy) Mock Test Series 2024 - NDA Mock Test: Mathematics - 9
Directions : Read the following information carefully and answer the questions given below.

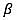 =
=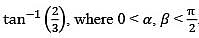
Q.
(α+ β) is equal to

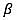 =
=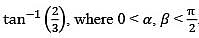
Suppose ω and ω2 are the complex cube root of unity which are given as
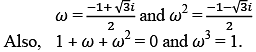
Q.
(1 – ω) (1 – ω2) (1 + ω4) (1 + ω8) is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Suppose ω and ω2 are the complex cube root of unity which are given as
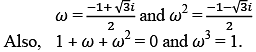
Q.
The value of expression
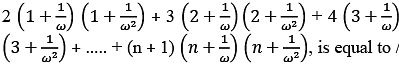
If 2x = 3 + 5i, then what is the 2x3 + 2x2 – 7x + 72?
285 is summation of 3 numbers. Ratio between 2nd and 3rd numbers is 6:5. Ratio between 1st and 2nd numbers is 3:7. The 3rdnumber is?
If α and β are the roots of the equation x2 + x + 1 = 0, then which of the following are the roots of the equation x2 – x + 1 = 0?
If the equation x2 – bx + 1 = 0 does not possess real roots, then which one of the following is correct?
Consider the equation (x – p) (x – 6) + 1 = 0 having integral coefficients. If the equation has integral roots, then what values can p have?
The roots of the equation (x – p) (x – q) = r2, where p, q and r are real, are
If A and B are two matrices such that AB = B and BA = A, then A2 + B2 is equal to
If A and B are two matrices of same order, then
Q.
(AB)n = AnBn is / (AB)n = AnBn
If A and B are two matrices of same order, then
Q.
If A and B are symmetric matrices, then (ABA)T is
The marked price of a watch is Rs. 800. A shopkeeper gives two successive discounts and sells the watch at Rs. 612. If the first discount is 10%, the second discount is
If each element in a row of a determinant is multiplied by the same factor r, then the value of the determinant
What is the value of where ω is the cube root of unity?
What is the value of sin A cos A tan A + cos A sin A cot A?
If cos A + cos B = m and sin A + sin B = n, where m, n ≠ 0, then what is sin (A + B) equal to?
If angles A, B and C are in AP, then what is sin A + 2 sin B + sin C equal to?
If p = sin (989o) cos (991o), then which one of the following is correct?
|
2 docs|101 tests
|
|
2 docs|101 tests
|