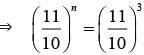All Courses
Get the App Signup / Login
Sign in Open App
Class 7 Exam  >  Class 7 Tests  >  Mathematics Olympiad Class 7  >  Olympiad Test: Compound Interest - Class 7 MCQ

Olympiad Test: Compound Interest - Class 7 MCQ


Test Description

20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Compound Interest

Olympiad Test: Compound Interest for Class 7 2024 is part of Mathematics Olympiad Class 7 preparation. The Olympiad Test: Compound Interest questions and answers have been prepared according to the Class 7 exam syllabus.The Olympiad Test: Compound Interest MCQs are made for Class 7 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Olympiad Test: Compound Interest below.
Solutions of Olympiad Test: Compound Interest questions in English are available as part of our Mathematics Olympiad Class 7 for Class 7 & Olympiad Test: Compound Interest solutions in Hindi for Mathematics Olympiad Class 7 course. Download more important topics, notes, lectures and mock test series for Class 7 Exam by signing up for free. Attempt Olympiad Test: Compound Interest | 20 questions in 40 minutes | Mock test for Class 7 preparation | Free important questions MCQ to study Mathematics Olympiad Class 7 for Class 7 Exam | Download free PDF with solutions
Olympiad Test: Compound Interest - Question 1
Save

Find compound interest on Rs 7500 at 4% per annum for 2 years, compounded annually.

Detailed Solution for Olympiad Test: Compound Interest - Question 1

Amount  = Rs [7500 × (1 + 4/100)²]
= Rs (7500 × 26/25 × 26/25)
= Rs 8112
C.I. = Rs (8112 – 7500)
= Rs 612

Olympiad Test: Compound Interest - Question 2
Save

Find the compound interest on Rs 16,000 at 20% per annum for 9 months, compounded quarterly.

Detailed Solution for Olympiad Test: Compound Interest - Question 2

Principal = Rs 16, 000;
Time = 9 months = 3 quarters;
Amount = Rs [16000 × (1+5/100)³]
= [16000 × 21/20 × 21/20 × 21/20]
= Rs 18522
C.I = Rs (18522 – 16000)
= Rs 2522

1 Crore+ students have signed up on EduRev. Have you? Download the App
Olympiad Test: Compound Interest - Question 3
Save

Simple interest on a certain sum of money for 3 years at 8% per annum is half the compound interest on Rs 4000 for 2 years at 10% per annum. The sum placed on simple interest is:

Detailed Solution for Olympiad Test: Compound Interest - Question 3

C.I. = Rs [4000 × (1+10/100)² – 4000]
= Rs (4000 × 11/10 × 11/10 – 4000)
= Rs 840
Sum = Rs [420 × 100 /3 × 8] = Rs 1750

Olympiad Test: Compound Interest - Question 4
Save

Anil invested an amount of Rs 8000 in a fixed deposit scheme for 2 years at compound interest rate 5% per annum. How much amount will Anil get on maturity of the fixed deposit?
Detailed Solution for Olympiad Test: Compound Interest - Question 4

Amount  = Rs [8000 × (1+5/100)²]
= Rs [8000 × 21/20 × 21/20]
= Rs 8820

Olympiad Test: Compound Interest - Question 5
Save

The present worth of Rs 169 due in 2 years at 4% per annum compound interest is:
Detailed Solution for Olympiad Test: Compound Interest - Question 5

Present worth = Rs [169/(1+4/100)²]
= Rs (169 × 25/26 × 25/26)
= Rs 156.25

Olympiad Test: Compound Interest - Question 6
Save

On a sum of money, the simple interest for 2 years is Rs 660, while the compound interest is Rs 696.30, the rate of interest being the same in both the cases. The rate of interest is:
Detailed Solution for Olympiad Test: Compound Interest - Question 6

Difference in C.I and S.I for 2 years
= Rs (6 96.30 – 660)
= Rs 36.30
S.I for one year =Rs 330
S.I on Rs 330 for 1 year = Rs 36.30
Rate = (100 × 36.30/330 × 1)% = 11% 

Olympiad Test: Compound Interest - Question 7
Save

The difference between simple interest and compound interest on Rs 1200 for one year at 10% per annum reckoned half yearly is
Detailed Solution for Olympiad Test: Compound Interest - Question 7

S.I = Rs  (1200 × 10 × 1/100)
= Rs 1 20
C.I = Rs  [1200 × (1+5/100)² – 1200]
= Rs 123
Difference = Rs [123 – 120] = Rs 3 

Olympiad Test: Compound Interest - Question 8
Save

A sum of money invested at compound interest amounts to Rs 800 in 3 years and to Rs 840 in 4 years. The rate of interest per annum is
Detailed Solution for Olympiad Test: Compound Interest - Question 8

S.I. on Rs 800 for 1 year = Rs [840 – 800]
= Rs 40
Rate = (100 × 40/800 × 1)%
= 5%

Olympiad Test: Compound Interest - Question 9
Save

If the simple interest on a sum of money for 2 years at 5% per annum is Rs 50, what is the compound interest on the same at the same rate and for the same time?
Detailed Solution for Olympiad Test: Compound Interest - Question 9

Sum = Rs (50 × 100/2×5)
= Rs 500
Amount = [Rs (500 × (1 + 5/100)²]
= Rs (500 × 21/20 × 21/20)
= Rs 551.25
C.I = Rs (551.25 – 500)
= Rs 51.25

Olympiad Test: Compound Interest - Question 10
Save

In what time will Rs 1000 become Rs 1331 at 10% per annum compounded annually?
Detailed Solution for Olympiad Test: Compound Interest - Question 10

Principal = Rs 1000
Amount = Rs 1331
Rate = Rs 10% p.a.
Let the time be n years. Then


Therefore n =  3 years.

Olympiad Test: Compound Interest - Question 11
Save

If the simple interest on a sum of money at 5% per annum for 3 years is Rs 1200, find the compound interest on the same sum for the same period at the same rate.
Detailed Solution for Olympiad Test: Compound Interest - Question 11

Clearly, Rate = 5% p.a.
Time = 3 years
S.I = Rs 1200.
So, Principal = Rs (100 × 1200/3× 5)
= Rs 8000
Amount = Rs [8000 × (1+ 5/100)³]
= Rs (8000 × 21/20 × 21/20 × 21/20)
= Rs 9261
C.I = Rs (9261 – 8000)
= Rs 1261

Olympiad Test: Compound Interest - Question 12
Save

What will be the compound interest on a sum of Rs 25,000 after 3 years at the rate of 12% per annum?
Detailed Solution for Olympiad Test: Compound Interest - Question 12

Amount = Rs (25000 × (1+12/100)³
= Rs (25000 × 28/25 × 28/25 × 28/25)
= Rs 35123.20.
C.I = Rs (35123.20 – 25000)
= Rs 10123.20

Olympiad Test: Compound Interest - Question 13
Save

The compound interest on Rs 30,000 at 7% per annum is Rs 4347. The period (in years) is
Detailed Solution for Olympiad Test: Compound Interest - Question 13

Amount = Rs (30000 + 4347)
= Rs 34347
Let the time be n years.
Then, 30000(1+7/100)n = 34347
⇒ (1+7/100)n  = 34347/3000
⇒ (107/100)n = 11449/1000
⇒(107/100)n = (107/100)2
Therefore  = 2 years

Olympiad Test: Compound Interest - Question 14
Save

The difference between compound interest and simple interest on an amount of Rs 15,000 for 2 years is Rs 96. What is the rate of interest per annum?
Detailed Solution for Olympiad Test: Compound Interest - Question 14

[15000 (1+ r/100)2 – 15000] – (15000 × r × 2)/100 = 96
By solving the above equation
r2 = (96 × 2)/3  = 64
Therefore r =  8%

Olympiad Test: Compound Interest - Question 15
Save

The compound interest on a certain sum for 2 years at 10% per annum is Rs 525. The simple interest on the same sum for double the time at half the rate percent per annum is:
Detailed Solution for Olympiad Test: Compound Interest - Question 15

Let the sum be Rs P.
Then, [P (1 + 10/100)2 – P] = 525
P = (11/10)2 – 1 = 525
P = (525 × 100)/21 = 2500
Therefore, sum = Rs 2500
S.I. = (2500 × 5 × 4)/100 = Rs 500

Olympiad Test: Compound Interest - Question 16
Save

At what rate of compound interest per annum will a sum of Rs 1200 become Rs 1348.32 in 2 years?
Detailed Solution for Olympiad Test: Compound Interest - Question 16

Let the rate be r% p.a.
Then, 1200 × (1 + R/100)2 =1348.32
(1 + R/100)2 = 11236/10000
(1 + R/100)2 = (106/100)2
Therefore r = 6%

Olympiad Test: Compound Interest - Question 17
Save

The least number of complete years in which a sum of money invested at 20% compound interest will be more than double is:
Detailed Solution for Olympiad Test: Compound Interest - Question 17

P(1 + 20/100)n > 2P (6/5)n > 2
Now, (6/5 × 6/5 × 6/5 × 6/5) > 2
So, n = 4 years

Olympiad Test: Compound Interest - Question 18
Save

The effective annual rate of interest corresponding to a nominal rate of 6% per annum payable half-yearly is:
Detailed Solution for Olympiad Test: Compound Interest - Question 18

Amount of Rs 100 for 1 year when compounded half-yearly
= Rs [100 × (1 + 3/100)2]
= Rs 106.09
Effective rate = (106.09 – 100)% = 6.09%

Olympiad Test: Compound Interest - Question 19
Save

There is 60% increase in an amount in 6 years at simple interest. What will be the compound interest of Rs 12,000 after 3 years at the same rate?
Detailed Solution for Olympiad Test: Compound Interest - Question 19

Let P = Rs 100. Then, S.I. Rs 60 and
T = 6 years.
∴ R = 100 × 60 / 100 × 6 = 10% p.a.
Now, P = Rs 12000 T = 3 years and
R = 10% p.a.
∴ C.I.  = Rs [12000 × (1 +10/100)3 – 1]
= 3972

Olympiad Test: Compound Interest - Question 20
Save

A bank offers 5% compound interest calculated on half-yearly basis. A customer deposits Rs 1600 each on 1st January and 1st July of a year. At the end of the year, the amount he would have gained by way of interest is:
Detailed Solution for Olympiad Test: Compound Interest - Question 20

Amount = [Rs1600 × (1 + 5/2 ×100)2 +Rs 1600 × (1 +5/2 ×100)]
= Rs 3321
∴ C.I.= Rs (3321 – 3200) = Rs 121

24 videos|57 docs|102 tests
Join Course
Information about Olympiad Test: Compound Interest Page
In this test you can find the Exam questions for Olympiad Test: Compound Interest solved & explained in the simplest way possible. Besides giving Questions and answers for Olympiad Test: Compound Interest, EduRev gives you an ample number of Online tests for practice

Top Courses for Class 7

24 videos|57 docs|102 tests
Join Course
Download as PDF

Top Courses for Class 7

Important Questions for Olympiad Test: Compound Interest

Find all the important questions for Olympiad Test: Compound Interest at EduRev.Get fully prepared for Olympiad Test: Compound Interest with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Olympiad Test: Compound Interest syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Olympiad Test: Compound Interest resources.

Olympiad Test: Compound Interest MCQs with Answers

Prepare for the Olympiad Test: Compound Interest within the Class 7 exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Olympiad Test: Compound Interest Mathematics Olympiad Class 7

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Olympiad Test: Compound Interest with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup