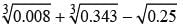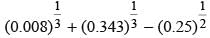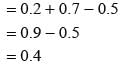Olympiad Test: Cube And Cube Roots - 1 - Class 8 MCQ
20 Questions MCQ Test - Olympiad Test: Cube And Cube Roots - 1
Which of the following numbers is a perfect cube?
What will be the volume of a cube having edge length 12m? (in m3)
What is the smallest number by which 576 is divided that quotient is a perfect cube?
If, 13 + 23 + 33 = (1 + 2 + 3)2, 13 + 23 + 33 + 43 = (1 + 2 + 3 + 4)2, then, 13 + 23 + 33 + 43 + 53 + 63 + 73
Observing the pattern 13 + 23 + 33 = (1 + 2 + 3)2, 13 + 23 + 33 + 43 = (1 + 2 + 3 + 4)2 , Find the sum:
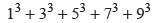
A natural number is of the form (3n + 2). Its cube will be of the form :
A real number ‘p’ is such that p > 1, then
Three numbers are in ratio 2 : 3 : 4 and sum of their cubes is 2673. The sum of these numbers are.
Which of the following is not a perfect cube?
The length of edge of a cube whose volume is 74.088 m3.
What is the smallest number by which 3087 may be multiplied so that the product is a perfect cube?
What is the smallest number by which 8788 must be divided so that the duotient is a perfect cube?
What is the smallest number by which 392 may be divided so that the duotient is a perfect cube?
Which of the following is a cube of odd numbers?
Which of the following is a cube of even numbers?




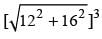
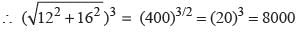

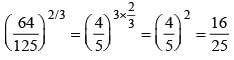
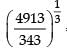 = ?
= ?