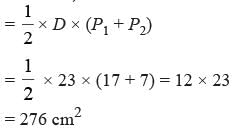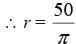Olympiad Test: Elementary Mensuration-I -2 - Class 7 MCQ
10 Questions MCQ Test - Olympiad Test: Elementary Mensuration-I -2
What is the area of a right-angled triangle?
I. The perimeter of the triangle is 30 cm.
II. The ratio between the base and the height of the triangle is 5 : 12.
III. The area of the triangle is equal to the area of a rectangle of length 10 cm.
I. The perimeter of the triangle is 30 cm.
II. The ratio between the base and the height of the triangle is 5 : 12.
III. The area of the triangle is equal to the area of a rectangle of length 10 cm.
What is the area of rectangular field?
I. The perimeter of the field is 110 metres.
II. The length is 5 metres more than the width.
III. The ratio between length and width is 6 : 5 respectively.
I. The perimeter of the field is 110 metres.
II. The length is 5 metres more than the width.
III. The ratio between length and width is 6 : 5 respectively.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the area of the given rectangle?
I. Perimeter of the rectangle is 60 cm.
II. Breadth of the rectangle is 12 cm.
III. Sum of two adjacent sides is 30 cm.
I. Perimeter of the rectangle is 60 cm.
II. Breadth of the rectangle is 12 cm.
III. Sum of two adjacent sides is 30 cm.
What is the cost of painting the two adjacent walls of a hall at Rs 5 per m2, which has no windows or doors?
I. The area of the hall is 24 sq. m.
II. The breadth, length and height of the hall are in the ratio of 4 : 6 : 5 respectively.
III. Area of one wall is 30 sq. m.
Find the area of the largest circle that can be drawn in a square of side 14 cm.
In a quadrilateral, the length of one of its diagonal is 23 cm and the perpendiculars drawn on this diagonal from other two vertices measure 17 cm and 7 cm respectively. Find the area of the quadrilateral.
The circumference of a circle is 100 cm. Find the side of the square inscribed in the circle.
If the radius of a circle is increased by 5%, find the percentage increase in its area.
If all sides of a hexagon is increased by 2%, find the percentage increase in its area.
If diameter of a circle is increased by 12%, find the percentage increase in its circumference.


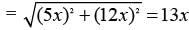
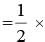 any diagonal × (sum of perpendiculars drawn on diagonal from two vertices)
any diagonal × (sum of perpendiculars drawn on diagonal from two vertices)