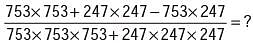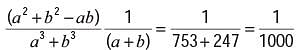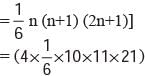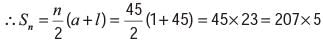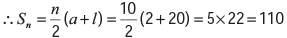Olympiad Test: Number System - 2 - Class 7 MCQ
20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Number System - 2
Which of the following is the unit digit in {(6374)1793 × (625)317 × (341491)}?
The last unit digit in the expansion of given expression 71n–1, where n is any positive integer is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the value of given number expression? 107 x 107 + 93 × 93 = ?
Which of the following is the remainder when we divide (6767 + 67) by 68?
Replace question mark with the suitable answer:
(12345679 × 2 × 62) = ?
Which of the following is the correct value of given number expression: (22 + 42 + 62 + ... + 202) = ?
What will be the sum of first forty five counting numbers?
What will be the sum of even numbers between 1 and 21 is?
What is the value obtained if we multiply 2056 and 987?
If two-third of three-fourth of a number is 30, then three – fifth of that number is:
What is the value of third integer if 3 times the first of 3 odd consecutive integers is three more than twice the third?
Find the value of given number expression: 397 × 397 + 104 × 104 + 2 × 397 × 104 = ?
Which of the following value is true in place of question mark? (35423 + 7164 + 41720) – (317 × 89) = ?
(an – bn) is completely divisible by (a – b), when
Find the divisor by which the given number expression (325 + 326 + 327 + 328) is completely divided.
When we divide a number say x by 6 it leaves a remainder 3. When we divide the square of the same number by 6, what will be the remainder?
Which of the following is the remainder when we divide 17200 by 18?
|
24 videos|57 docs|102 tests
|
|
24 videos|57 docs|102 tests
|