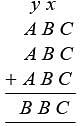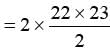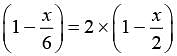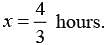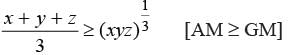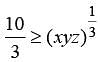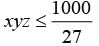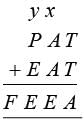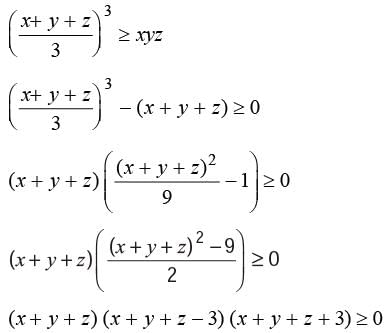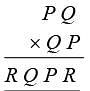Olympiad Test: Playing With Numbers - 2 - Class 8 MCQ
20 Questions MCQ Test - Olympiad Test: Playing With Numbers - 2
763*312, which number should the * be replaced to make the number divisible by 9?
76215*, the replacement of * by a number gives a number which is divisible by 11, the number will be :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
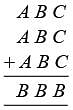 , the values of A, B, C are digits from 1 to 9. What will be value of B?
, the values of A, B, C are digits from 1 to 9. What will be value of B?
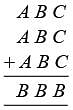 , the values of A, B, C are digits from 1 to 9. What will be value of B?
, the values of A, B, C are digits from 1 to 9. What will be value of B?What will be the sum of first 22 natural numbers, which, are even?
One candle was guaranteed to burn for 6 hours, the other for 2 hours. They were both lit at same time. After some time one candle was twice as long as the other. For how long had they been burning?
Which is a 3-digit numbers, such that all its digits are prime and the 3 digits are the factors of the number?
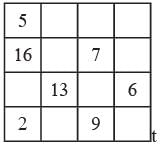
Complete the square given below, and find the value of the sum of missing numbers. The sum of the magic square is 34.
Three numbers are such that their sum is 10 and their product is maximum. The product will be :
What will be the one’s place digit of 6222?
Find the smallest number which can be expressed as the sum of two cubes of natural numbers.
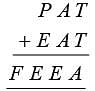 , where, P, A, T, E, F are digits from to what will be the value of F?
, where, P, A, T, E, F are digits from to what will be the value of F?
Sum of 3 numbers = product of 3 numbers. If the numbers are consecutive and natural. Find the triplet having least value, of their sum.
The square of a number is having 5 at its units place and 2 at its tenths place, then the least natural number having these properties are :
Which of the following number is not a perfect squares ?
26 + 34 × 17 ÷ 4 = 34, which of the two signs should be interchanged to get the desired result?
Which is the least number divisible by 2, 3, 5 and 55 ?
What is the square number just greater than 60, which can be expressed as a sum of two successive triangular numbers?
What is the value of P if P, Q, R are replaced by digits from 1 to 9? PQ × QP = RQPR.