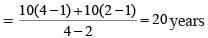Olympiad Test : Problems On Ages - Class 6 MCQ
20 Questions MCQ Test - Olympiad Test : Problems On Ages
Present ages of Sameer and Anand are in the ratio of 5 : 4 respectively. Three years hence, the ratio of their ages will become 11 : 9 respectively. What is Anand’s present age in years?
A is two years older than B who is twice as old as C. If the total of the ages of A, B and C be 27, then how old is B?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A father said to his son, “I was as old as you are at the present at the time of your birth”. If the father’s age is 38 years now, the son’s age five years back was:
The sum of ages of 5 children born at the intervals of 3 years each is 50 years. What is the age of the youngest child?
Father is aged three times more than his son Ronit. After 8 years, he would be two and a half times of Ronit’s age. After further 8 years, how many times would he be of Ronit’s age?
The age of father 10 years ago was thrice the age of his son. Ten years hence, father’s age will be twice that of his son. The ratio of their present ages is:
Q is as much younger than R as he is older than T. If the sum of the ages of R and T is 50 years, what is definitely the difference between R and Q’s age?
A person’s present age is two-fifth of the age of his mother. After 8 years, he will be onehalf of the age of his mother. How old is the mother at present?
Ayesha’s father was 38 years of age when she was born while her mother was 36 years old when her brother four years younger to her was born. What is the difference between the ages of her parents?
The present ages of three persons are in proportions 4 : 7 : 9. Eight years ago, the sum of their ages was 56. Find their present ages (in years).
A man is 24 years older than his son. In two years, his age will be twice the age of his son. The present age of his son is:
Six years ago, the ratio of the ages of Kunal and Sagar was 6 : 5. Four years hence, the ratio of their ages will be 11 : 10. What is Sagar’s age at present?
The sum of the present ages of a father and his son is 60 years. Six years ago, father’s age was five times the age of the son. After 6 years, son’s age will be:
At present, the ratio between the ages of Arun and Deepak is 4 : 3. After 6 years, Arun’s age will be 26 years. What is the age of Deepak at present?
Sachin is younger than Rahul by 7 years. If their ages are in the respective ratio of 7 : 9, how old is Sachin?
The ratio of the father’s age to the son’s age is 4 : 1. The product of their ages is 196. What will be the ratio of their ages after 5 years?
The ratio of Rita’s age to the age of her mother is 3 : 11. The difference of their ages is 24 years. What will be the ratio of their ages after 3 years?
The sum of ages of a mother and her daughter is 50 years. Also 5 years ago, the mother’s age was 7 times the age of the daughter. What are the present ages of the mother and the daughter?
The sum of the ages of a son and a father is 56 years. After 4 years, the age of the father will be three times that of the son. What is the age of the son?
10 years ago, Sita’s mother was 4 times older than her daughter. After 10 years, the mother will be two times older than the daughter. What is the present age of Sita?