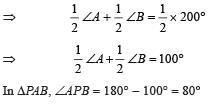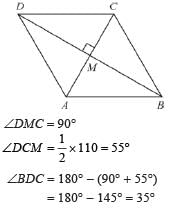Olympiad Test: Quadrilaterals - 1
20 Questions MCQ Test Mathematical Olympiad Class 8 | Olympiad Test: Quadrilaterals - 1
| 1 Crore+ students have signed up on EduRev. Have you? |
The four angles of a quadrilateral are in the ratio 2 : 3 : 5 : 8. Then what is the difference between largest and smallest angle of the quadrilateral?
Let the angles are 2x, 3x, 5x, 8x.
∴ 2x + 3x + 5x + 8x = 360°
⇒ 18x = 360° ⇒ x = 20°
2x = 2 × 20° = 40°; 3x = 3 × 20° = 60°
5x = 5 × 20° = 100°; 8x = 8 × 20° = 160°
Required difference = 160° - 40° = 120°.
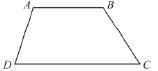
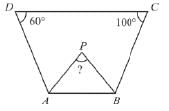
In the given figure the bisector of ∠A and ∠B meet in a point P. If ∠C = 100°, ∠D = 60°, what is the the measure of ∠APB?
In figure ∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠B + 100° + 60° = 360°
⇒ ∠A + ∠B = 200°
Three angles of a quadrilateral are equal and the measure of fourth angle is 120°. What is the measure of each of the equal angle?
Let the angle be x.
∴ x + x + x + 120° = 360°
⇒ 3x = 240° ⇒ x = 80°
The length of diagonals of a rhombus are 16 cm and 12 cm respectively. What is the length of each of its sides?
Here ABCD is a rhombus and in ∆AOD
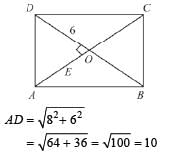
The sum of two opposite angles of a parallelogram is 130°. What is the difference between largest and smallest angle of parallelogram?
Here ABCD is a parallelogram and ∠A + ∠C = 130°
∠B = ∠D = 115°
Difference = 115° - 65° = 50°
The bisectors of any two adjacent angles of a parallelogram intersect at
If one angle of a parallelogram is 24° less than twice the smallest angle then what is the value of largest angle of the parallelogram?
Let ∠A be the smallest angle.
The ratio of two sides of a parallelogram is 4 : 3. If its perimeter is 56 cm, what is the difference between largest and smallest side?
The opposite sides of parallelogram are equal.
∴ 4x + 3x + 4x + 3x = 56
⇒ 14x = 56 ⇒ x = 4
∴ 4x = 4 × 4 = 16
and 3x = 4 × 3 = 12
∴ Difference = 16 – 12 = 4 cm
In the given Fig. ABCD is a rhombus. If ∠DAB = 110°, what is ∠BDC ?
In rhombus ABCD,
∠DAB = 110° = ∠BCD
Two adjacent sides of a parallelogram are 5 cm and 7 cm long what is the perimeter of parallelogram?
Perimeter of parallelogram
= 5 + 7 + 5 +7 = 24 cm
Of any two adjacent sides of a parallelogram one is longer than the other by 3 cm. If the perimeter is 36 cm, then what is the length of smaller side of parallelogram?
Let smaller side be x.
Longer side = x +3
∴ x + x + 3 + x + x + 3 = 36
⇒ 4x + 6 = 36 ⇒ 4x = 30
ABCD is a rhombus, AC = 16 cm and BD = 12 cm, then what is the measure of BC?
∵ ABCD is a rhombus.
∴ AB = BC = CD = DA
∵ Diagonals of a rhombus bisect each other.
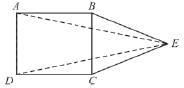
In ∆BCE, BE = EC, and ABCD is a square, and ∠BEC = 60°, then the measure of ∠BEA will be :
Given BE = EC
∴ ∠EBC = ∠ECB
In ∆BEC,
2∠EBC + ∠BEC = 180°
⇒ ∠EBC = ∠ECB = 60°
∴ ∆EBC is an equilateral triangle having
EB = BC = EC
AB = BC = CD = DA = EB = EC
[∵ABCD is a square].
∠ABE = 90° + 60° = 150°
In ∆ABE,
∠ABE + 2∠AEB = 180° [Q AEB = BAE].
2∠AEB = 180° - ∠ABE = 180 - 150 = 30°
⇒ ∠AEB = 15°
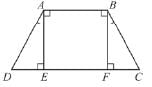
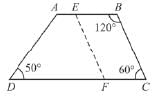
From the adjoining figure, find the measure of ∠EFD if AB || CD, EF || BC.
∠ABC + ∠BCF = 180°
[Interior angles or same side of transversal].
⇒ ∠BCF =180° - 120° = 60°
∠BCF = ∠EFD (corresponding angles)
∴ ∠EFD = 60°
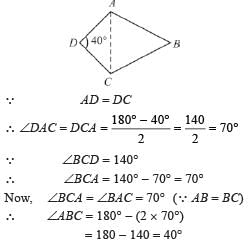
In the adjoining figure ABCD, AB = DC and AB = BC and, ∠ADC = 40° and ∠BCD = 140°, then, ∠ABC =
Joining A to C,
ABCD is a parallelogram having its sides, AB = 4x + 1 BC = 2y + 3, CD = 25, DA = y + 28, then, x + y =
In a parallelogram.
AB = CD, and, BC = DA
⇒ 4x + 1 = 25 and 2y + 3 = y + 28
⇒ x = 6, and, y = 25
∴ x + y = 6 + 25 = 31
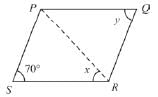
PQRS is a parallelogram and ∠SPR = 50°, then find y.
PQRS is a parallelogram.
∴ ∠S = ∠Q = y = 70°
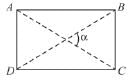
If α < 90°, then, ABCD, may be a : (Given : ABCD is a parallelogram) and ∠B = 90°
∵ ∠B = 90°, and, ABCD is a parallelogram
∴ ∠C = 90°, ∠A = 90° and ∠D = 90°
So, ABCD may be a rectangle or square, but, since, α < 90°.
∴ΑΒCD must be a rectangle.
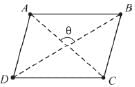
If θ = 90°, and, ∠A = ∠C = 110°, then, ABCD is :
∵ θ = 90° (Angle between the diagonals)
∴ ABCD may be a rhombus or square.
But, since, ∠A = ∠C = 110°
∴ ABCD must be a rhombus.
In a rhombus or any parallelogram, the opposite angles are always equal
ABCD is an isosceles trapezium , i.e., AD = BC, then
∵ ABCD is an isosceles trapezium.
∴ AD = BC
Draw AE ⊥ DC and BF ⊥ DC, then, in ∆AED and ∠BFC.
∠AED = ∠BFC = 90°,
AB = BC,
AE = BF (perpendicular distance between two parallel lines)
∴ ∆AEB ≅ ∆BFC (ets congruency)
∴ ∠A = ∠B
|
16 videos|76 docs|56 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
16 videos|76 docs|56 tests
|
Download free EduRev App
Related content with Olympiad Test: Quadrilaterals - 1
|
|
|
Related tests with Olympiad Test: Quadrilaterals - 1
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
