Olympiad Test: The Triangle and Its Properties - JSS 2 MCQ
20 Questions MCQ Test - Olympiad Test: The Triangle and Its Properties
In a ΔABC, if AB2=BC2+AC2,at which vertex is the right angle?
Which type of triangle is formed by BC=7.2cm, AC=6 cm and ∠120o?
In the Pythagoras property, the triangle must be ___________ .
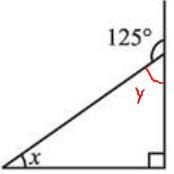
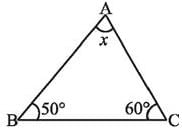
Find the value of x in this figure.
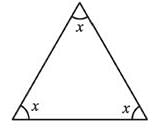
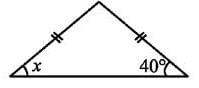
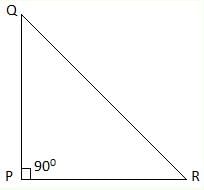
Find the value of x in given figure.

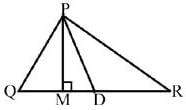
In ΔPQR, D is the midpoint of QR. Then, PD is
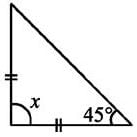
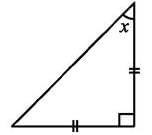
The value of x in the adjoining figure is
If the two legs of a right angled triangle are equal and the square of the hypotenuse is 100 sq units, what is the length of each leg?
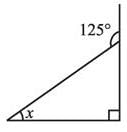
Find the value of unknown x in the adjoining figure.
ΔABC is right-angled at C. If AC = 5 cm and BC = 12 cm find the length of AB.
ΔPQR is a triangle right-angled at P. If PQ = 3 cm and PR = 4 cm, find QR.
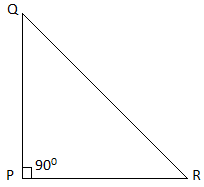
Which is the longest side in the triangle PQR right angled at P?
The value of x in the adjoining figure is
A triangle in which all three sides are of equal lengths is called _________.
If the angles of a triangle are in the ratio 1:2:7,what type of a triangle is it?
In a triangle, an exterior angle is always equal to __________.
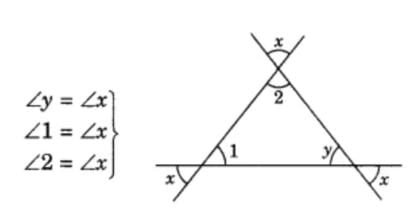
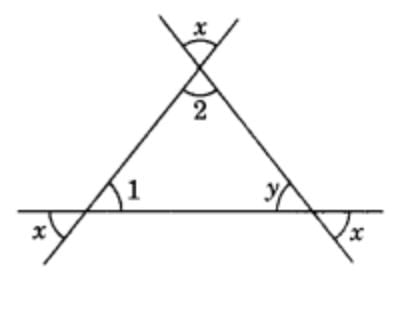
Find value of angle 1, 2, and 3, where angle y is equal to angle 3
If a triangle has angles measuring 40°, 60°, and x°, find the value of x.