Oscillations - Online Test (05-01-2017) - Class 11 MCQ
30 Questions MCQ Test - Oscillations - Online Test (05-01-2017)
Out of the following functions representing motion of a particle
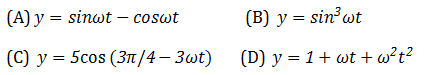
Which represent SHM:
A particle of mass m is released from rest and follows a parabolic path as shown in figure
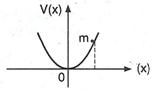
Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
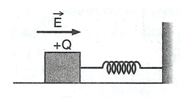
A wooden block performs SHM on a frictionless surface with frequency v0. The block carries a charge +Q on its surface. If now a uniform electric field  is switched on as shown in fig. then the SHM of the block will be:
is switched on as shown in fig. then the SHM of the block will be:
An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. the piston and cylinder have equal cross-sectional area A. when the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surroundings, the piston executes a simple harmonic motion with frequency:
A mass M, attached to a horizontal spring, executes SHM with amplitude A1. When the mass M passes through its mean position, then a smaller mass m is placed over it and both of them move together with amplitude A2. The ratio of (A1/A2) is :
Two sound waves are respectively
y1= asin(ωt -kx) and y2 = bcos(ωt -kx).
The phase difference between the two waves is :
a particle moves in XY-plane according to the rule x=asinωt and y=acosωt the particle follows:
The displacement of a particle along X-axis is given by x= asin2ωt. The motion of the particle corresponds to
In damped oscillations, the amplitude of oscillations is reduced to one-third of its initial value a0 at the end of 100 oscillations. When the oscillator completes 200 oscillations, its amplitude must be:
The amplitude of a damped oscillator decreases to 0.9 times its original magnitude in 5s. in another 10s, it will decrease to ∝ times its original magnitude, where ∝ equals:
What is the time period of a simple pendulum whose point of suspension is moving horizontally with an acceleration of a inside an accelerated vehicle
A simple pendulum has a period T. it is taken inside a lift moving up with uniform acceleration g/3. now its time period will be
The shape of l - T graph of simple pendulum is,
. Two waves are represented by the equations y1 = a sin(ωt + kx + 0.57)m and y2 = a cos (ωt + kx)m, where x is in metre and time is in second. The phase difference between them is
The period of oscillation of the mass M suspended from a spring of negligible mass is T. if along with another mass M is also suspended, the period of oscillation will now be
Which one of the following equations of motion represents simple harmonic motion?
A particle of mass m executes simple harmonic motion with amplitude a and frequency u. The average kinetic energy during its motion from the position of equilibrium to the end is
Two springs of force constant k1 and k2 are connected to a mass m as shown. The frequency of oscillation of the mass is f. if both k1 and k2 are made four time their original values, the frequency of oscillation becomes
A body of mass 8 kg is suspended through two light springs X and Y connected in series. The readings in X nad Y are respectively
The resultant spring constant of the system of springs shown is
The mass M shown in figure oscillates in SHM with amplitude A. the amplitude of the point P is :
If x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then which of the following does not change with time:
The displacement of a particle along X-axis is given by x=asin2 ωt . The motion of the particle corresponds to:
In damped oscillations, the amplitude of oscillations is reduced to one-third of its initial value a0 at the end of 100 oscillations. When the oscillator completes 200 oscillations, its amplitude must be:
A simple pendulum has a time period T1. The point of suspension is now moved upwards according to the relation : y=kt2,(k=1m/s2) where y is the vertical displacement. The time period now becomes T2. The ratio is: (g = 10 m/s2)
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 s. the frequency of the wave is:
A pendulum clock is observed to give correct time at the equator. What will happen if the same pendulum clock is taken to the pole of the earth?

















