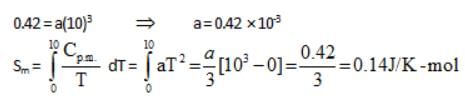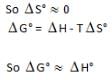P. Bahadur Test: Thermodynamics - NEET MCQ
25 Questions MCQ Test - P. Bahadur Test: Thermodynamics
Consider the reaction at 300K
H2(9) + Cl2(9) → 2HCI(g), ΔH° = — 185 KJ
If 3 mole of HE completely react with 3 mol of CI2 to form CI, AU° of the reaction will be
H2(9) + Cl2(9) → 2HCI(g), ΔH° = — 185 KJ
It has been observed that the ratio of the molar heat of vaporisation of liquid and its normal boiling point is approximately same for most of the liquids (called Triton's rule) Which of the following does not follow this rule
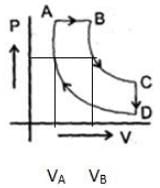
A cyclic proces ABCD is shown in PV diagram for an ideal gas.
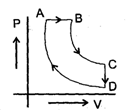
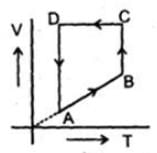
Which of the following diagram represents the same process
The change in free energy accompanied by the isothermal reversible expansion of 1 mol of an ideal gas when it doubles its volume is ΔG1 The change in free energy accompanied by sudden isothermal irreversible doubling volume of 1 mole of the same gas is ΔG2 Ratio of ΔG1 and ΔG2
The following curve represents the variation of Gibbs function 'G' with pressure at constant temperature.
Correct match of given plots with the physical state of a substance is
Which of the following diagram correctly represents the variation of internal energy (U) of gas under expansion at constant temperature.
Which correctly represents the entropy (s) of an isolated system during a process
Which of the following represents positive work i.e. work of compression
For a perfectly crystalline solid Cp m = aT3, where a is constant. If a is 0.42 J/K-mol at 10 K, molar entropy at 10 K is
One mole of an ideal monoatomic gas expands isothermally against constant external pressure of 1 atm from initial volume of 1L to a state where its final pressure becomes equal to external pressure. If initial temperature of gas is 300 K then total entropy change of system in the above process is :
[R = 0.082 L atm mol-1 K-1 = 8.3 J mo1-1K-1].
At 1000 K water vapour at 1 atm. has been found to be dissociated into H2 and 02 to the extent of 3 x 10-6 %.Calculate the free energy decrease of the system, assuming ideal behaviour.
In the reaction COCl2(g) C0(g) + CI2(g) at 550°, when the initial pressure of CO & Cl2 are 250 and 280 mm of Hg respectively. The equilibrium pressure is found to be 380 mm of Hg. Calculate the degree of dissociation of COC12 at 1 atm. What will be the extent of dissociation, when N2 at a pressure of 0.4 atm is present and the total pressure is 1 atm.
When 1 mole of an ideal gas at 20 atm pressure and 15 L volume expands such that the final pressure becomes 10 atm and the final volume become 60 L. Calculate entropy change for the process (Cpm = 30.96 J mole-1 K-1)
An ideal gas is taken from the same initial pressure P1 to the same final pressure P2 by three different processes. If it is known that point 1 corresponds to a reversible adiabatic and point 2 corresponds to a single stage adiabatic the
Which of the following graphs best illustrates the variation of entropy of a substance with temp.
During winters, moisture condenses in the form of dew and can be seen on plant leaves and grass. The entropy of the system in such cases decreases as liquids possess lesser disorder as compared to gases. With reference to the second law, which statement is correct, for the above process ?
A copper block of mass `m' at temperature 'T1' is kept in the open atmosphere at temperature `T2' where T2 > T1 . The variation of entropy of the copper block with time is best illustrated by
For which process will AHD° and AG° be expected to be most similar.
Statement-1 : Due to adiabatic free expansion temperature of real gas may increase
Statement-2 : In adiabatic free expansion, temperature is always constant irrespective of real or ideal gas
Statement-1 : Under free expansion , 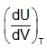 is + ve when attractive forces are dominant between gas dB molecules [U, V, T respresent internal energy, volume and temperature of gas respectively]
is + ve when attractive forces are dominant between gas dB molecules [U, V, T respresent internal energy, volume and temperature of gas respectively]
Statement-2 Internal energy is a state function.
The enthalpy of fusion of water is 1.435 kcal/mol. The molar entropy change for the melting of ice at 0°C is
Statement-1 : 'Diamonds are forever is generally quoted for diamond as rate of conversion of diamond to graphite at room condition is nearly zero.
Statement-2 : At room condition, conversion of diamond into graphite is spontaneons.
Statement-1 : At low temperature, ΔH is the dominant factor for spontaneity of a reaction.
Statement-2 : The opposing factor TΔS remains very small, at low temperature.
Statement-1 : The amount of work done in the isothermal expansion is greater than work done in the adiabatic system for same final volume.
Statement-2 : In the adiabatic expansion of a gas temperature and pressure both decrease due to decrease in internal energy of the system.
Statement-1 : The heat absorbed during isothermal expansion of an ideal gas against vacuum is zero.
Statemept-2 : In isothermal process, change in internal energy is always zero, irrespective of ideal or real gas.