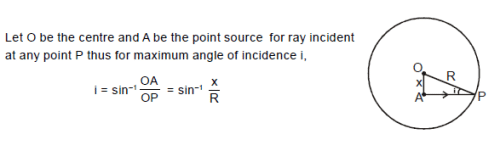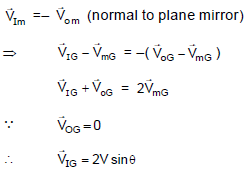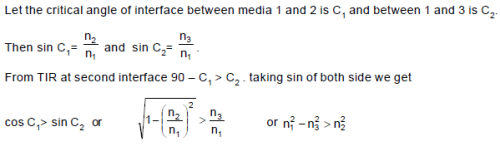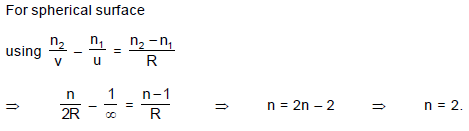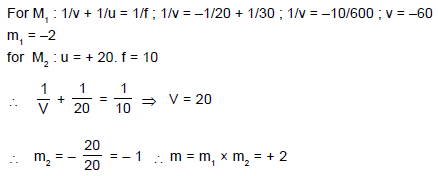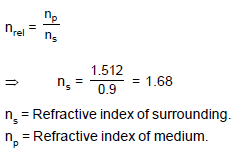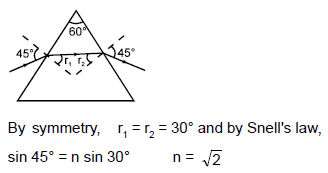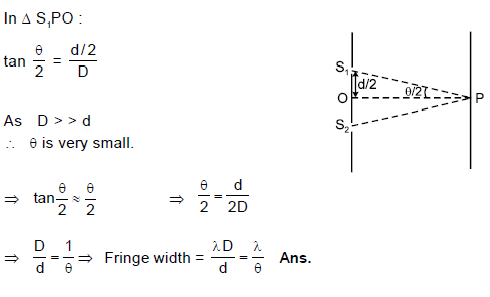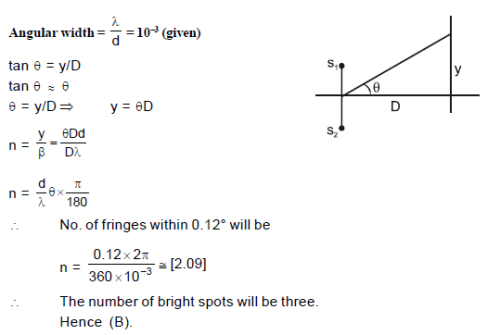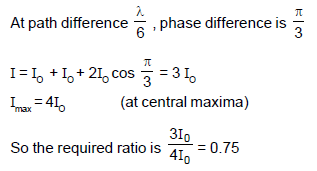Part Test- 4 (JEE Main 2018) - JEE MCQ
30 Questions MCQ Test - Part Test- 4 (JEE Main 2018)
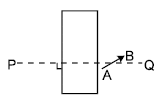
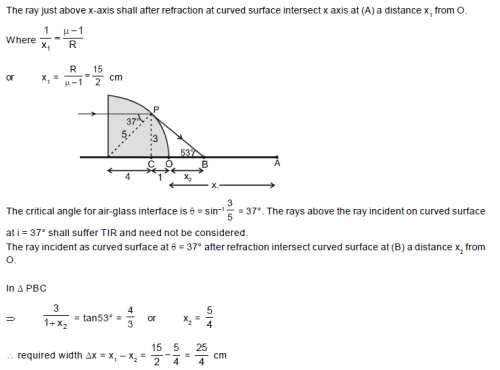
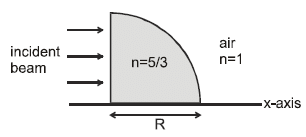
A uniform, horizontal parallel beam of light is incident upon a prism as shown. The prism is in the shape of a quarter cylinder, of radius R = 5 cm, and has the index of refraction n = 5/3. The width of the region at which the incident rays after normal incidence on plane surface and subsequent refraction at curved surface intersect on x axis is (Neglect the ray which travels along x-axis as shown in figure)
Inside a solid glass sphere of radius R , a point source of light lies at a distance x ( x < R) from centre of the sphere. The solid sphere is surrounded by air of refractive index 1. The maximum angle of incidence for rays incident on the spherical glass- air interface directly from the point source is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two transparent slabs are of equal length (thickness). One is made of a material A of R.I. 1.5 and the other is made of materials B and C, the ratio of their thickness being 1: 2. The R.I. of C is 1.6. When light passes through them, the two slabs have the same number of waves. The R.I. of B is (Light is incident normally)

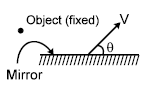
An object moves in front of a fixed plane mirror. The velocity of the image of the object is
An object and a plane mirror are shown in figure. Mirror is moved with velocity V as shown. The velocity of image is :
The rainbow formed after or during the rain is due to
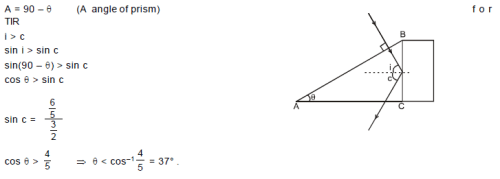
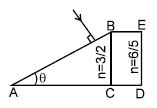
In the figure ABC is the cross section of a right angled prism and BCDE is the cross section of a glass slab. The value of θ so that light incident normally on the face AB does not cross the face BC is (given sin–1 (3/5) = 37º)
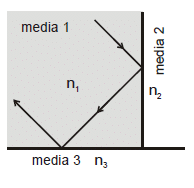
In the diagram shown, light is incident on the interface between media 1 (refractive index n1) and 2 (refractive index n2) at angle slightly greater than the critical angle and is totally reflected. The light is then also totally reflected at the interface between media 1 and 3 (refractive index n3) after which it travels in a direction opposite to its initial direction. The media must have a refractive indices such that
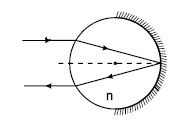
A transparent cylinder has its right half polished so as to act as a mirror. A paraxial light ray is incident from left, that is parallel to principal axis, exits parallel to the incident ray as shown. The refractive index n of the material of the cylinder is :
A prism of refractive index of √2 has a refracting angle of 60°. At what angle must a ray be incident on it so that it suffers a minimum deviation?
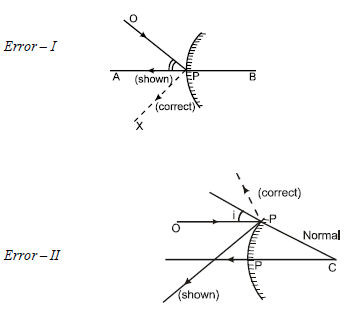
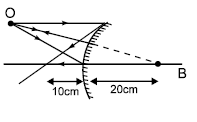
In the figure shown a convex mirror of radius of curvature 20 cm is shown. An object O is placed in front of this mirror. Its ray diagram is shown. How many mistakes are there in the ray diagram (AB is its principal axis):
For a real object, all of the following statements are correct except :
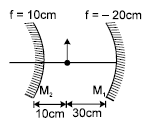
In the figure shown find the total magnification after two successive reflections first on M1 & then on M2
A particle revolves in clockwise direction (as seen from point A) in a circle C of radius 1 cm and completes one revolution in 2 sec. The axis of the circle and the principal axis of the mirror M coincide. Call it AB. The radius of curvature of the mirror is 20 cm. Then the direction of revolution (as seen from A) of the image of the particle and its speed is

The relative refractive index of glass with respect to a material is 0.9 and the absolute refractive index of glass is 1.512. The refractive index of the material is
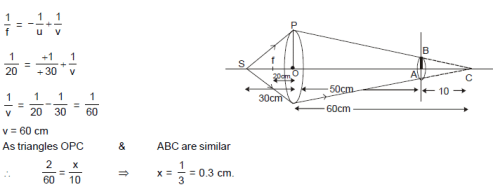
A lens of focal length 20.0 cm and aperture radius 2.0 cm is placed at a distance 30.0 cm from a point source of light. On the other side a screen is placed at a distance 50.0 cm from the lens. The radius of spot of light formed on screen is. (Neglect spherical abberation through lens)
A convex lens is cut into two parts in different ways that are arranged in four manners, as shown. Which arrangement will give maximum optical power ?
A ray of light is incident at an angle of incidence 45º on an equilateral prism and emerge at an angle 45º then the refractive index of the medium of the prism is :
The distance of nth bright fringe to the (n+1)th dark fringe in Young's experiment is equal to:
In a Young's double slit experiment, d = 1 mm, λ = 6000 Å and D = 1 m (where d, λ and D have usual meaning). Each of slit individually produces same intensity on the screen. The minimum distance between two points on the screen having 75 % intensity of the maximum intensity is :
Let S1 and S2 be the two slits in Young’s double slit experiment. If central maxima is observed at P and angle S1PS2 = θ, then the fringe width for the light of wavelength λ will be. (Assume θ to be a small angle)
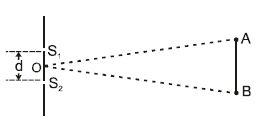
Figure shows two coherent sources S1-S2 vibrating in same phase. AB is an irregular wire lying at a far distance from the sources S1 and S2. = 0.12°. How many bright spots will be seen on the wire, including points A and B.
If the ratio of the intensity of two coherent sources is 4 then the visibility [(Imax- Imin)/(Imax+ Imin)] of the fringes is
In Young’s double slit experiment, we get 60 fringes in the field of view of monochromatic light of wavelength 4000 A0. If we use monochromatic light of wavelength 6000 A0, then the number of fringes that would be obtained in the same field of view is :
If the distance between the first maxima and fifth minima of a double slit pattern is 7mm and the slits are separated by 0.15 mm with the screen 50 cm from the slits, then wavelength of the light used is
The path difference between two interfering waves at a point on the screen is λ/6. The ratio of intensity at this point and that at the central bright fringe will be : (Assume that intensity due to each slit is same)
In a Young’s double slit experiment, the separation between the slits is d, distance between the slit and screen is D (D >> d). In the interference pattern, there is a maxima exactly in front for each slit. Then the possible wavelengths used in the experiment are :
A point source of light is kept at the centre of a solid transparent sphere. The sphere is surrounded by air . The refractive index of material of sphere for which the rays incident from point source on glass–air interface will suffer total internal reflection is:
A point object ' O ' is at the centre of curvature of a concave mirror. The mirror starts to move at a speed u, in a direction perpendicular to the principal axis. Then the initial velocity of the image is:
In the figure shown an object ‘AB’ makes small angle with the normal line ‘PQ’. The length of ‘AB’ is l. The refractive index of the slab is ‘n’ and the surrounding medium is air. ‘AB’ is seen with the help of paraxial rays, from the left side of the slab. The size of the image of AB is