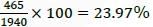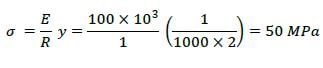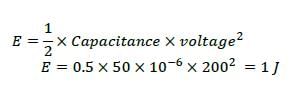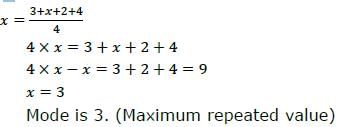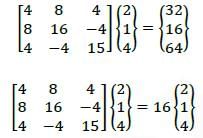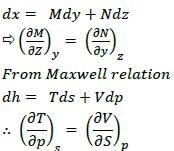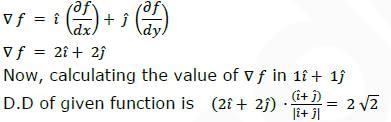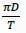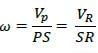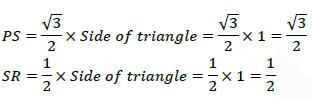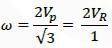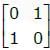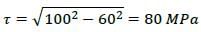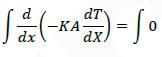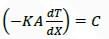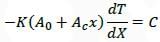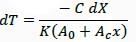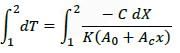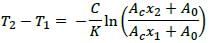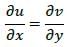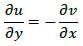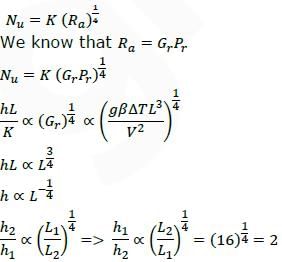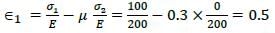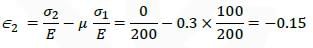Past Year Paper - Mechanical Engineering GATE : 2019 - Mechanical Engineering MCQ
30 Questions MCQ Test - Past Year Paper - Mechanical Engineering GATE : 2019
A final examination is the __________ of a series of evaluations that a student has to go through.
If IMHO = JNIP; IDK = JEL; and SO = TP, then IDC = __________.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Are there enough seats here? There are __________ people here than I expected.
Once the team of analysts identify the problem, we ________ in a better position to comment on the issue.Which one of the following choices CANNOT fill the given blank?
The product of three integers X, Y and Z is 192. Z is equal to 4 and P is equal to the average of X and Y. What is the minimum possible value of P?
X is an online media provider. By offering unlimited and exclusive online content at attractive prices for a loyalty membership, X is almost forcing its customers towards its loyalty membership. If its loyalty membership continues to grow at its current rate, within the next eight years more households will be watching X than cable television.Which one of the following statements can be inferred from the above paragraph?
Fiscal deficit was 4% of the GDP in 2015 and that increased to 5% in 2016. If the GDP increased by 10% from 2015 to 2016, the percentage increase in the actual fiscal deficit is ____________.
Two pipes P and Q can fill a tank in 6 hours and 9 hours respectively, while a third pipe R can empty the tank in 12 hours. Initially, P and R are open for 4 hours. Then P is closed and Q is opened. After 6 more hours R is closed. The total time taken to fill the tank (in hours) is _________.
While teaching a creative writing class in India, I was surprised at receiving stories from the students that were all set in distant places: in the American West with cowboys and in Manhattam penthouses with clinking ice cubes. This was, till an eminent cAribbean writer gave the writers in the once-colonised countries the confidence to see the shabby lives around them as worthy of being “told”.The writer of this passage is surprised by the creative writing assignments of his students, because __________.
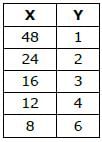
Mola is a digital platform for taxis in a city. It offers three types of rides – Pool, Mini and Prime. The Table below presents the number of rides for the past four months. The platform earns one US dollar per ride. What is the percentage share of revenue contributed by Prime to the total revenues of Mola, for the entire duration?

A wire of circular cross-section of diameter 1.0 mm is bent into a circular arc of radius 1.0 m by application of pure bending moments at its ends. The Young’s modulus of the material of the wire is 100 GPa. The maximum tensile stress developed in the wire is ____________ MPa.
In an electrical discharge machining process, the breakdown voltage across inter electrode gap (IEG) is 200 V and the capacitance of the RC circuit is 50 μF. The energy (in J) released per spark across the IEG is __________
If x is the mean of data 3, x, 2 and 4, then the mode is _________
The cold forming process in which a hardened tool is pressed against a workpiece (when there is relative motion between the tool and the workpiece) to produce a roughened surface with a regular pattern is
Endurance limit of a beam subjected to pure bending decreases with
In matrix equation [A] {X} = {R}.
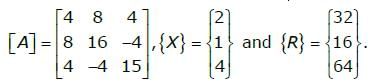
One of the eigenvalues of matrix [A] is
Water enters a circular pipe of length L = 5.0 m and diameter D = 0.20 m with Reynolds number
ReD = 500. The velocity profile at the inlet of the pipe is uniform while it is parabolic at the exit.
The Reynolds number at the exit of the pipe is___________.
For a simple compressible system, v, s, p and T are specific volume, specific entropy, pressure
and temperature, respectively. As per Maxwell’s relations, 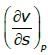 is equal to
is equal to
Hardenability of steel is a measure of
The directional derivative of the function f(x, y) = x2 + y2 along a line directed from (0, 0) to (1,
1), evaluated at the point x = 1, y = 1 is
A spur gear has pitch circle diameter D and number of teeth T. The circular pitch of the gear is
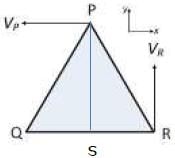
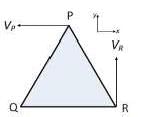
A rigid triangular body, PQR, with sides of equal length of 1 unit moves on a flat plane. At the
instant shown, edge QR is parallel to the x-axis, and the body moves such that velocities of
points P and R are VP and VR, in the x and y directions, respectively. The magnitude of the
angular velocity of the body is
Sphere 1 with a diameter of 0.1 m is completely enclosed by another sphere 2 of diameter 0.4
m. The view factor F12 is
The transformation matrix for mirroring a point in x – y plane about the line y = x is given by
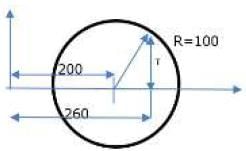
The state of stress at a point in a component is represented by a Mohr’s circle of radius 100 MPa centered at 200 MPa on the normal stress axis. On a plane passing through the same point, the normal stress is 260 MPa. The magnitude of the shear stress on the same plane at the same point is ___________ MPa.
One-dimensional steady state heat conduction takes place through a solid whose cross-sectional area varies linearly in the direction of heat transfer. Assume there is no heat generation in the solid and the thermal conductivity of the material is constant and independent of temperature. The temperature distribution in the solid is
An analytic function f(z) of complex variable z = x + l y may be written as f(z) = u(x, y) + iv (x,
y). Then, u(x, y) and v(x, y) must satisfy
A thin vertical flat plate of height L, and infinite width perpendicular to the plane of the figure, is
losing heat to the surroundings by natural convection. The temperatures of the plate and the
surroundings, and the properties of the surrounding fluid, are constant. The relationship between
the average Nusselt and Rayleigh numbers is given as Nu = K Ra ¼, where K is a constant. The
length scales for Nusselt and Rayleigh numbers are the height of the plate. The height of the
plate is increased to 16L keeping all other factors constant.
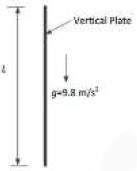
If the average heat transfer coefficient for the first plate is h1 and that for the second plate is h2,
the value of the ratio h1/h2 is____________.
Which one of the following modifications of the simple ideal Rankine cycle increases the thermal efficiency and reduces the moisture content of the steam at the turbine outlet?
Consider a linear rectangular thin sheet of metal, subjected to uniform uniaxial tensile stress of 100 MPa along the length direction. Assume plane stress conditions in the plane normal to the thickness. The Young’s modulus E = 200 MPa and Poisson’s ratio v = 0.3 are given. The principal strains in the plane of the sheet are


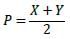
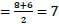
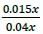 ×100=37.5%
×100=37.5%