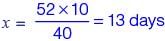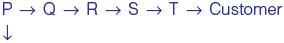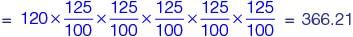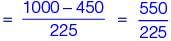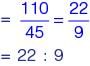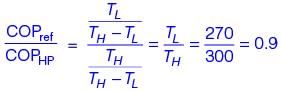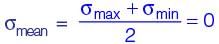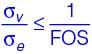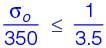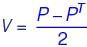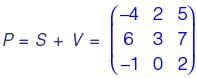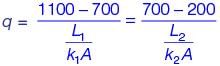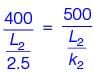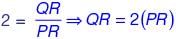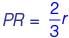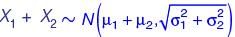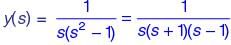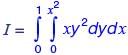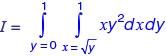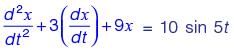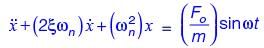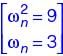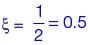Past Year Paper - Mechanical Engineering GATE : 2020 (Session - 2) - Mechanical Engineering MCQ
30 Questions MCQ Test - Past Year Paper - Mechanical Engineering GATE : 2020 (Session - 2)
The recent measures to improve the output would ______ the level of production to our satisfaction.
It was estimated that 52 men can complete a strip in a newly constructed highway connecting cities P and Q in 10 days. Due to an emergency, 12 men were sent to another project. How many number of days, more than the original estimate, will be required to complete the strip?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An engineer measures THREE quantities X, Y and Z in an experiment. She finds that they follow a relationship that is represented in the figure below: (the product of X and Y linearly varies with Z )
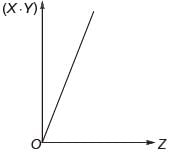
Then, which of the following statements is FALSE?

Then, which of the following statements is FALSE?
While I agree ________ his proposal this time, I do not often agree ______ him.
Select the word that fits the analogy:
White : Whitening : : Light : ________.
There are five levels {P, Q , R, S, T ) in a linear supply chain before a product reaches customers, as shown in the figure.
At each of the five levels, the price of the product is increased by 25%. If the product is produced at level P at the cost of Rs. 120 per unit, what is the paid (in rupees) by the customers?
In one of the greatest innings ever seen in 142 years of Test history. Ben Stokes upped the tempo in a five-and-a-half hour long stay of 219 balls including 11 fours and 8 sixes that saw him finish on a 135 not out as England squared the five-match series.Based on their connotations in the given passage, which one of the following meanings DOES NOT match?
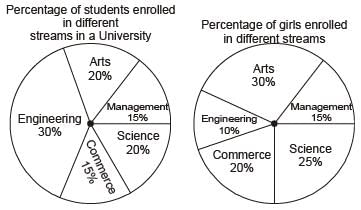
The two pie-charts given below show the data of total students and only girls registered in different streams in a university. If the total number of students registered in the university is 5000, and the total number of the registered girls is 1500; then, the ratio of boys enrolled in Arts to the girls enrolled in Management is __________.
Climate change and resilience deal with two aspects - reduction of sources of nonrenewable energy resources and reducing vulnerability of climate change aspects. The terms 'mitigation' and 'adaptation' are used to refer to these aspects, respectively.
Which of the following assertions is best supported by the above information?
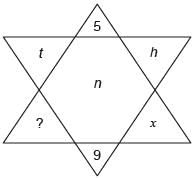
Find the missing element in the following figure:
For an air-standard Diesel cycle,
The number of qualitatively distinct kinematic inversions possible for a Grashof chain with four revolute pairs is
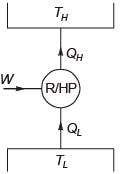
If a reversed Carnot cycle operates between the temperature limits of 27°C and –3°C, then the ratio of the COP of a refrigerator to that of a heat pump (COP of refrigerator/ COP of heat pump) based on the cycle is __________ (round off to 2 decimal places).
A machine member is subjected to fluctuating stress σ = σ0cos(8πt). The endurance limit of the material is 350 MPa. If the factor of safety used in the design is 3.5 then the maximum allowable value of σ0 is __________ MPa (round off to 2 decimal places).
The process, that uses a tapered horn to amplify and focus the mechanical energy for machining of glass, is
In Materials Requirement Planning, if the inventory holding cost is very high and the setup cost is zero, which one of the following lot sizing approaches should be used?
A matrix P is decomposed into its symmetric part S and skew symmetric part V. If
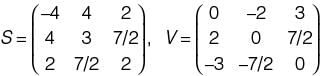
then matrix P is
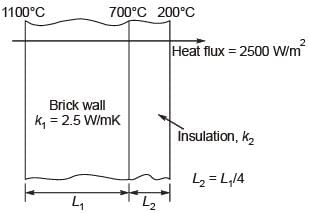
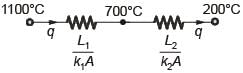
In a furnace, the inner and outer sides of the brick wall (k1 = 2.5 W/mK) are maintained at 1100°C and 700°C respectively as shown in figure.

The brick wall is covered by an insulating material of thermal conductivity k2. The thickness of the insulation is 1/4th of the thickness of the brick wall. The outer surface of the insulation is at 200°C. The heat flux through the composite walls is 2500 W/m2.
The value of k2 is ________ W/mK (round off to 2 decimal places).
Which of the following conditions is used lo determine the stable equilibrium of all partially submerged floating bodies?
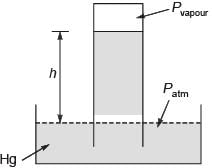
In the space above the mercury column in a barometer tube, the gauge pressure of the vapour is
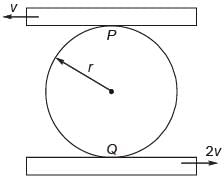
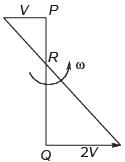
A circular disk of radius r is confined to roll without slipping at P and Q as shown in the figure.
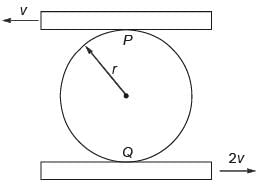
If the plates have velocities as shown, the magnitude of the angular velocity of the disk is
The sum of two normally distributed random variables X and Y is
The solution of 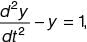 which additionally satisfies
which additionally satisfies 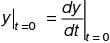 = 0 in the
= 0 in the
Laplace s-domain is
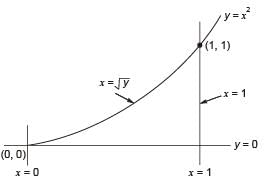
Let 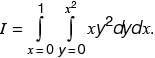 then, I may also be expressed as
then, I may also be expressed as
A closed vessel contains pure water, in thermal equilibrium with its vapour at 25°C (Stage #1), as shown.
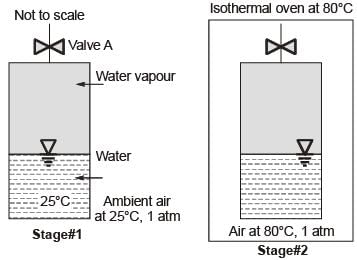
The vessel in this stage is then kept inside an isothermal oven which is having an atmosphere of hot air maintained at 80°C. The vessel exchanges heat with the oven atmosphere and attains a new thermal equilibrium (Stage #2). If the Valve A is now opened inside the oven, what will happen immediately after opening the valve?
Let I be a 100 dimensional identity matrix and E be the set of its distinct (no value appears more than once in E) real eigenvalues. The number of elements in E is ______.
A bolt head has to be made at the end of a rod of diameter d = 12 mm by localized forging (upsetting) operation. The length of the unsupported portion of the rod is 40 mm.
To avoid buckling of the rod, a closed forging operation has to be performed with a maximum die diameter of ________ mm.
The values of enthalpies at the stator inlet and rotor outlet of a hydraulic turbomachine stage are h1 and h3 respectively. The enthalpy at the stator outlet (or, rotor inlet) is h2.The condition (h2 – h1) = (h3 – h2) indicates that the degree of reaction of this stage is
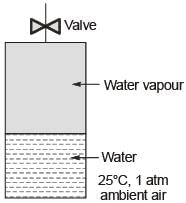
The figure below shows a symbolic representation of the surface texture in a perpendicular lay orientation with indicative values (I through VI) marking the various specifications whose definitions are listed below.
P: Maximum Waviness Height (mm);
Q: Maximum Roughness Height (mm);
R: Minimum Roughness Height (mm);
S: Maximum Waviness Width (mm);
T: Maximum Roughness Width (mm);
U: Roughness Width (mm);
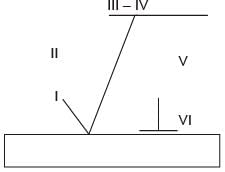
The correct match between the specifications and the symbols (I to VI) is:
The equation of motion of a spring-mass-damper system is given by
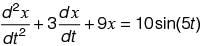
The damping factor for the system is