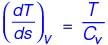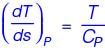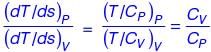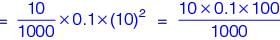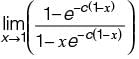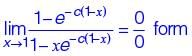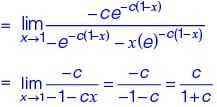Past Year Paper - Mechanical Engineering GATE : 2020 (Session - 1) - Mechanical Engineering MCQ
30 Questions MCQ Test - Past Year Paper - Mechanical Engineering GATE : 2020 (Session - 1)
He is known for his unscrupulous ways. He always sheds _______ tears to deceive people.
The bar graph shows the data of the students who appeared and passed in an examination for four schools P, Q, R and S. The average of success rates (in percentage) of these four schools is __________.

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Select the graph that schematically represents BOTH y = xm and y = x1/m properly in the interval 0 ≤ x ≤ 1. For integer values of m, where m > 1.
Define [x ] as the greatest integer less than or equal to x, for each x ∈(–∞, ∞). If y = [x], then area under y for x ∈[1, 4] is _______.
P, Q, R and S are to be uniquely coded using α and β. If P is coded as αα and Q as αβ, then R and S, respectively, can be coded as ________.
Crowd funding deals with mobilisation of funds for a project from a large number of people, who would be willing to invest smaller amounts through web-based platforms in the project. Based on the above paragraph, which of the following is correct about crowd funding?
Jofra Archer, the England fast bowler, is _______ than accurate.
Select the word that fits the analogy:
Build : Building : : Grow : _______
I do not think you know the case well enough to have opinions. Having said that, I agree with your other point. What does the phrase “having said that” mean in the given text?
The sum of the first n terms in the sequence 8, 88, 888, 8888, .... is ______.
For three vectors 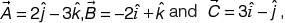 where
where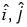 are unit vectors along the axes of a right-handed rectangular/Cartesian coordinate system, the value of
are unit vectors along the axes of a right-handed rectangular/Cartesian coordinate system, the value of 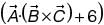 is __________.
is __________.
He compressor of a gas turbine plant, operating on an ideal intercooled Brayton cycle, accomplishes an overall compression ratio of 6 in a two-stage compression process, Intercooling is used to cool the air coming out from the first stage to the inlet temperature of the first stage, before its entry to the second stage. Air enters the compressor at 300 K and 100 kPa. If the properties of gas are constant, the intercooling pressure for minimum compressor work is________ kPa (round off to 2 decimal places).
The Laplace transform of a function f (t) is L(f ) = 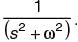 Then, f(t) is
Then, f(t) is
Match the following.

A single-degree-of-freedom oscillator is subjected to harmonic excitation F (t) = F0cos(ωt ) as shown in the figure.
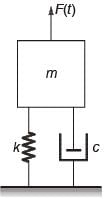
The non-zero value of ω, for which the amplitude of the force transmitted to the ground will be F0, is
For an ideal gas, the value of the Joule-Thomson coefficient is
He stress state at a point in a material under plane stress condition is equi-biaxial tension with a magnitude of 10 MPa. If one unit on the σ – π plane is 1 MPa, the Mohr's circle representation of the state-of-stress is given by
The base of a brass bracket needs rough grinding. For this purpose, the most suitable grinding wheel grade specification is
Which of the following function f (z), of the complex variable z , is NOT analytic at all the points of the complex plane?
Multiplication of real valued square matrices of same dimension is
A company is hiring to fill four managerial vacancies. The candidates are five men and three women. If every candidate is equally likely to be chosen then the probability that at least one women will be selected is _______ (round off to 2 decimal places).
In a concentric tube counter-flow heat exchanger, hot oil enters at 102°C and leaves at 65°C. Cold water enters at 25°C and leaves at 42°C. The log mean temperature difference (LMTD) is _______°C (round off to one decimal place).
A flywheel is attached to an engine to keep its rotational speed between 100 rad/s and 110 rad/s. If the energy fluctuation in the flywheel between these two speeds is 1.05 kJ then the moment of inertia of the flywheel is _________________kg.m2 (round off to 2 decimal places).
In the Critical Path Method (CPM), the cost-time slope of an activity is given by
A sheet metal with a stock hardness of 250 HRC has to be sheared using a punch and a die having a clearance of 1 mm between them. If the stock hardness of the sheet metal increases to 400 HRC, the clearance between the punch and the die should be_________ mm.
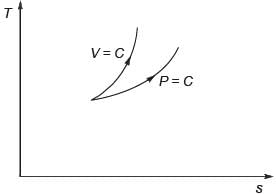
For an ideal gas, a constant pressure line and a constant volume line intersect at a point, in the Temperature (T) versus specific entropy (s) diagram. CP is the specific heat at constant pressure and CV is the specific heat at constant volume. The ratio of the slopes of the constant pressure and constant volume lines at the point of intersection is
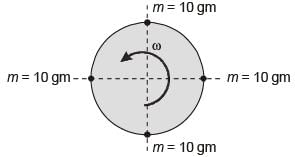
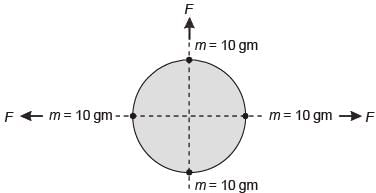
A balanced rigid disc mounted on a rigid rotor has four identical point masses, each of 10 grams, attached to four points on the 100 mm radius circle shown in the figure
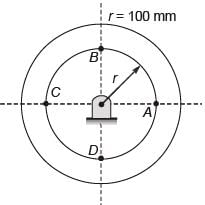
The rotor is driven by a motor at uniform angular speed of 10 rad/s. If one of the masses gets detached then the magnitude of the resultant unbalance force on the rotor is ______ N. (round off to 2 decimal places).
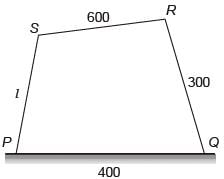
A four bar mechanism is shown below.
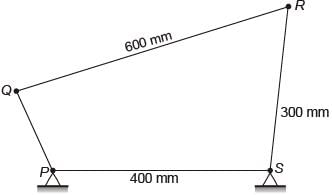
For the mechanism to be a crank-rocker mechanism, the length of the link PQ can be
A helical gear with 20° pressure angle and 30° helix angle mounted at the mid-span of a shaft that is supported between two bearings at the ends. The nature of the stresses induced in the shaft is





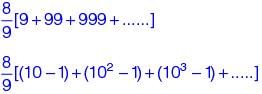
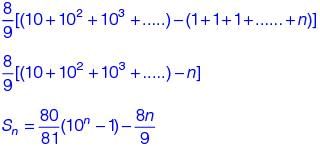
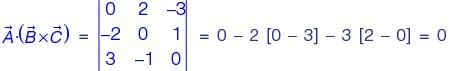
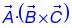 + 6 = 0 + 6 = 6
+ 6 = 0 + 6 = 6
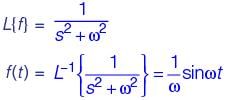
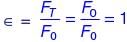

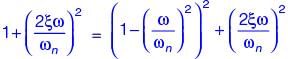
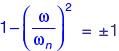
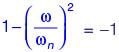
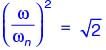
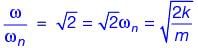
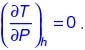
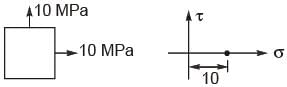
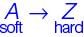
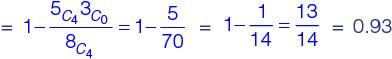
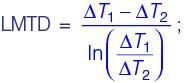
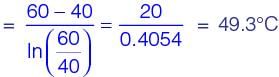
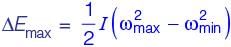
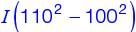


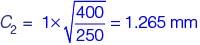
 If
If