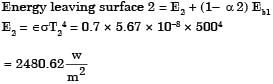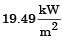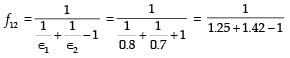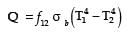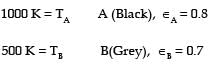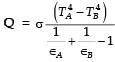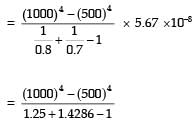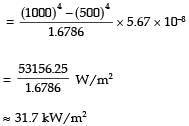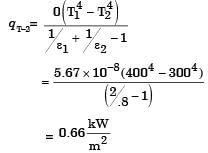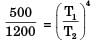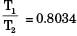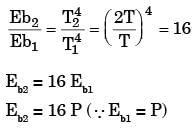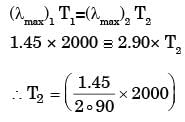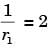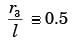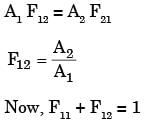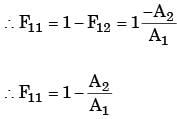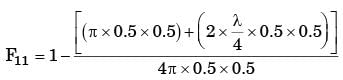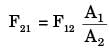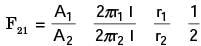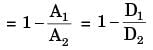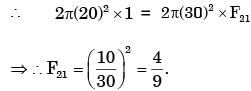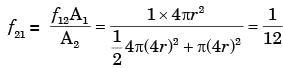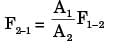Past Year Questions: Radiation - Mechanical Engineering MCQ
23 Questions MCQ Test Additional Study Material for Mechanical Engineering - Past Year Questions: Radiation
For a glass plate transmissivity and reflectivity are specified as 0.86 and 0.08 respectively, the absorptivity of the glass plate is
[1988]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the value of the view factor for two inclined flat plates having common edge of equal length and wlth an angle of 20 degrees?
[2002]
The following figure was generated from experimental data relating spectral black body emissive power to wave length at the three temperatures T1, T2 and T3( T1 > T2 >T3).
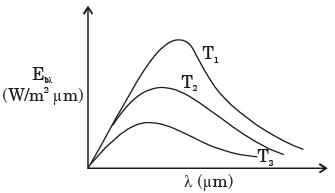
The conclusion in that the measurements are
[2005]
For an opaque surface, the absorptivity (α), transmissivity (τ) and reflectivity (ρ) are related by the equation
[2012]
The radiative heat transfer rate per unit area (W/m2) between two plane parallel gray surfaces (emissivity = 0.9) maintained at 400 K and 300 K is (σ = Stefan Boltzmann constant = 5.67 × 10-8 W/m2K4)
[1993]
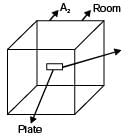
A plate having 10 cm2 area each side is hanging in the middle of a room of 100 m2 total surface area. The plate temperature and emissivity are respectively 800 K and 0.6. The temperature and emissivity valute for the surfaces of the room are 300 K and 0.3 respectively. Boltzmann's constant σ = 5.67 × 10-8 W/m2K4. The total heat loss from the two surfaces of the plate is
[2003]
A100 W electric bulb was switched on in a 2.5 m × 3 m × 3 m size thermally insulated room having a temperature of 20°C. The room temperature at the end of 24 hours will be
[2006]
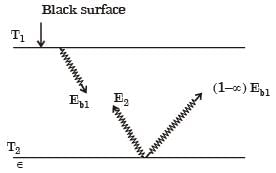
Radiative heat transfer is intercepted between the inner surfaces of two very large isothermal parallel metal plates. While the upper plate (designated as plate 1) is a black surface and is the warmer one being maintained at 727°C, the lower plate (plate 2) is a diffuse and gray surface with an emissivity of 0.7 and is kept at 227°C. Assume that the surfaces are sufficiently large to form a two-surface enclosure and steady-state conditions to exist. Stefan-Boltzmann constant is given as 5.67 × 10–8 W/m2K4.
The irradiation (in kW/m2) for the plate (plate 1) is
[2009]
Radiative heat transfer is intercepted between the inner surfaces of two very large isothermal parallel metal plates. While the upper plate (designated as plate 1) is a black surface and is the warmer one being maintained at 727°C, the lower plate (plate 2) is a diffuse and gray surface with an emissivity of 0.7 and is kept at 227°C. Assume that the surfaces are sufficiently large to form a two-surface enclosure and steady-state conditions to exist. Stefan-Boltzmann constant is given as 5.67 × 10–8 W/m2K4.
If plate 1 is also a diffuse and gray surface with an emissivity value of 0.8, the net radiatibn heat exchange (in kW/m2) between plate 1 and plate 2 is
[2009]
Two larged if fuse gray parallel plates, separated by a small distance, have surface temperature of 400 K and 300 K. If the emissivities of the surfaces are 0.8 and the Stefan-Boltzmann constant is 5.67 × 10–8 W/ m2K4, the net radiation heat exchange rate in kW/m2 between the two plates is
[2013]
The total emissive power of a surface is 500 W/ m2 at temperature T1 and 1200 W/m2 at emperature T2, where the temperature are in Kelvin. Assuming the emissivity of the surface to be constant, the ratio of the temperature T1/T2 is
[2015]
The emissive power of a blackbody is P. If its absolute temperature is doubled, the emissive power becomes
[2017]
The peak wavelength of radiation emitted by a black body at a temperature of 2000 K is 1.45 μm. If the peak wavelength of emitted radiation changes to 2.90 μm , then the temperature (in K) of the black body is
[2018]
For the circular tube of equal length and diameter shown in figure below, the view factor F13 is 0.17. The view factor F12 in this case will be

[2001]
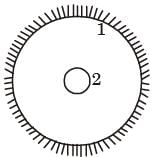
A solid cylinder (surface 2) is located at the centre of a hollow sphere (surface 1). The diameter of the sphere is 1 m, while the cylinder has a diameter and length of 0.5 m each.'The radiation configuration factor F11 is
[2005]
A hollow enclosure is formed between two inf initely long concentric cylinders of radii 1 m and 2 m, respectively. Radiative heat exchange takes place between the inner surface of the larger cylinder (surface-2) and the outer surface of the smaller cylinder (surface-1). The radiating surface are diffuse and the medium in the enclosure is non- participating. The fraction of the thermal radiation leaving the larger surface and striking itself is
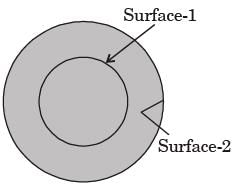
[2008]
Consider two infinitely long thin concentric tubes of circular cross section as shown in figure. If D1 and D2 are the diameters of the inner and outer tubes respectively, then the view factor F22 is given by
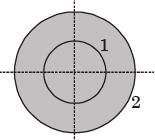
[2012]
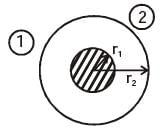
A solid sphere of radius r1 = 20 mm is placed concentrically inside a hollow sphere of radius r2 = 30 mm as shown in the figure.
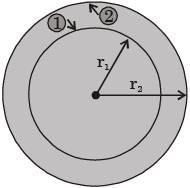
The view factor F21 for radiation heat transfer is
[2014]
A solid sphere 1 of radius r is placed inside a hollow, closed hemispherical surface 2 of radius 4r. The shape factor F is,
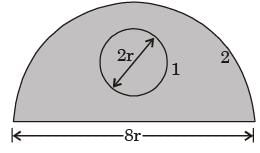
[2015]
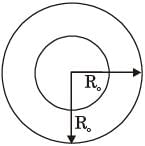
Consider the radiation heat exchange inside an annulus between two very long concentric cylinders. The radius of the outer cylinder is R0 and that of the inner cylinder is Ri. The radiation view factor of the outer cylinder onto itself is
[2016]
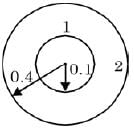
Sphere 1 with a diameter of 0.1 m is completely enclosed by another sphere 2 of diameter 0.4 m.The view factor F12 is
[2019]
Two infinite parallel plates are placed at a certain distance apart. An infinite radiation shield is inserted between the plates without touching any of them to reduce heat exchange between the plates. Assume that the emissivities of plates and radiation shield are equal. The ratio of the net heat exchange between the plates with and without the shield is
[2014]
|
1 videos|30 docs|57 tests
|
|
1 videos|30 docs|57 tests
|


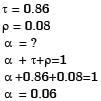
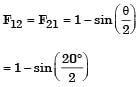
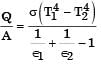
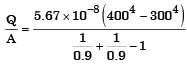
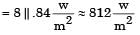
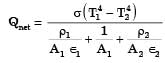
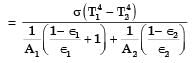
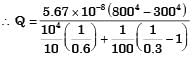 = 13.66 W
= 13.66 W